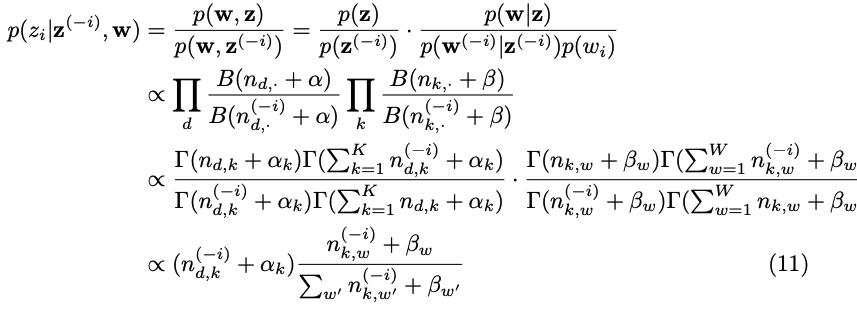CS6220 Unsupervised Data Mining

HW5B Topic Models LDA, Sampling

Make sure you check the syllabus for the due date. Please use the notations adopted in class, even if the problem is stated in the book using a different notation.

We are not looking for very long answers (if you find yourself writing more than one or two pages of typed text per problem, you are probably on the wrong track). Try to be concise; also keep in mind that good ideas and explanations matter more than exact details.

Submit all code files Dropbox (create folder HW1 or similar name). Results can be pdf or txt files, including plots/tabels if any.

"Paper" exercises: submit using Dropbox as pdf, either typed or scanned handwritten.

DATATSET : 20 NewsGroups : news articles

PROBLEM 1: Simple Sampling

You are not allowed to use sampling libraries/functions. But you can use rand() call to generate a pseudo-uniform value in [0,1]; you can also use a library that computes the pdf(x|params). make sure to recap first Rejection Sampling and Inverse Transform Sampling
A. Implement simple sampling from continuous distributions: uniform (min, max, sample_size) and gaussian (mu, sigma, sample_size)
B. Implement sampling from a 2-dim Gaussian Distribution (2d mu, 2d sigma, sample_size)
C. Implement wihtout-replacement sampling from a discrete non-uniform distribution (given as input) following the Steven's method described in class ( paper ). Test it on desired sample sizes N significantly smaller than population size M (for example N=20 M=300)

PROBLEM 2: Conditional Sampling

Implement Gibbs Sampling for a multidim gaussian generative joint, by using the conditionals which are also gaussian distributions . The minimum requirement is for joint to have D=2 variables and for Gibbs to alternate between the two.

PROBLEM 3: Implement your own baby-LDA

Implement your own LDA using Gibbs Sampling, following this paper and this easy-to-read book . Gibbs Sampling is a lot slower than EM alternatives, so this can take some time; use a smaller sample of docs/words at first.
20NG train dataset 11280 docs x 53000 words
Small sonnet dataset (one per line) 154 docs x 3092 words

% clean text for stopwords, frequent words, short words, numerical words etc.
%N docs, K topics, W words, length(d)=# of words in doc d, DLMAX= max doc length
%N x DLMAX matrix DOCS[d,i]=w : i-th word in doc d is w (w is an index in Vocab dictionary)
% alternatively to DOCS one can use Dx W matrix X[d,w] = count of word w in doc d
% Wx1 array Vocab[w] = actual word string

% set number of topics >
K=6

% N x K matrix A[d,k] : count of times topic k is sampled for doc d
% K x W matrix B[k,w] : count of times topic k is sampled for word w

% 1 x K array alpha : dirichlet uniform prior of doc over topics; below 5-1=4 is the strength of the prior
alpha = 5*ones(1,K)

% 1 x W array beta: dirichlet unif prior of topic over words; 2-1=1 is the strength of the prior
beta = 2*ones(1, W)

% N x DLMAX matrix Z[d,i] = k ; topic k currently sampled for i-th word in doc d; initially zero = no topic
Z=zeros(D,DLMAX)

% start A as alpha prior for each doc (each row is alpha)
A = repmat (alpha, N, 1)

% start B as beta prior for each topic (each row is beta)
B = repmat (beta, K, 1)

% K x 1 array BSUM = sum of B over all words, per topic
BSUM = sum(B,2)

%resample topic for each word in each doc, T=1000 iterations
for each iteration T=1:1000
for each doc d=1:D
for each index i=1:length(d)
   w = DOCD(d,i) %the word
   zi = Z(d,i) % current topic

   % subtract current topic zi from counts
   if (zi>0)
     A(d,zi) = A(d,zi) -1
     B(zi,w) = B(zi,w) -1
     BSUM(zi) = BSUM(zi) -1
   end_if

   %prepare Gibbs-sampling cond distribution over topics prob(zi=k | all-else-sampled)
   %dist (unnormalized) is A(d_row) .* B(k_column)-normalized-k
   ".*" is product for each component, example [2 3 -1] .* [2 8 2] = [ 4 24 -2]
   dst = A(d,:) .* (B(:,w) ./ BSUM)'
   % this calculation corresponds to the derivation below( LDA simplified ), where n_dk is our A and n_kw is our B

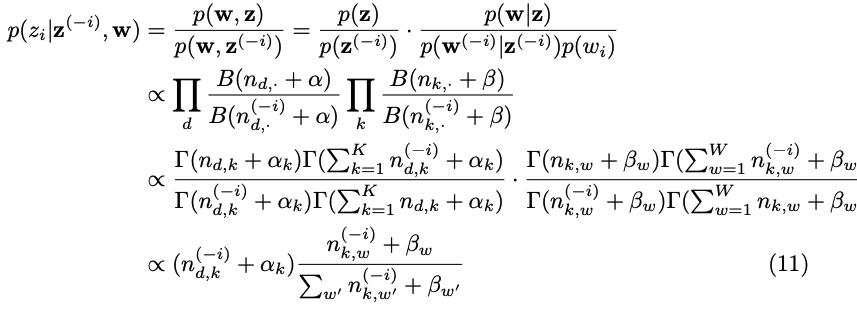
   %sample a new topic from nonuniform discrete dst over topics ;
   %you can use a built-in function or do binary-search over cdf(dst)
   new_zi = randsample(dst)
   %update Z and counts
   Z(d,i)= new_zi
   A(d,new_zi) = A(d,new_zi) +1
   B(new_zi,w) = B(new_zi,w) + 1
   BSUM(new_zi) = BSUM(new_zi) +1
end_for_loops

% each row in A is the doc d distribution over topics (unnormalized)
% each row in B is the topic k distribution words (unnormalized)

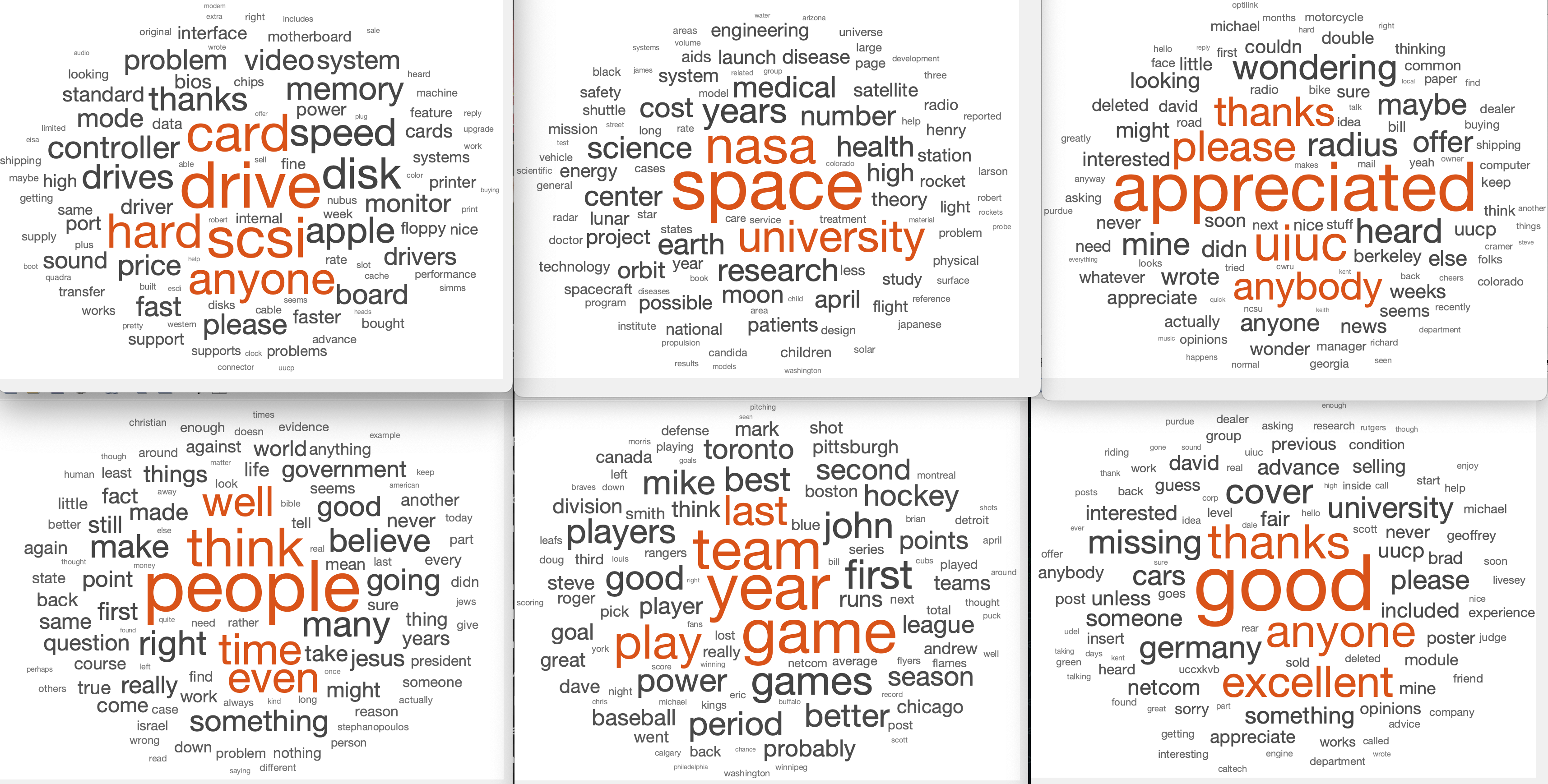
% display a "wordcloud" for each topic, using B for word weights
for k=1:K
   figure(k); clf;
   wordcloud(Vocab, B(k,:));
end_for