We extend, and finalize, our memory model for Java programs, and discuss garbage collection. We use our memory model to introduce Java programs that use mutation and circular data structures. We discuss the effects of mutation and circular data structure to our programs covering stack overflow exceptions and equality between objects.
We introduce class invariants and use pre-conditions and post-conditions along with invariants to reason about Java programs that use mutation.
- Write the names of the two types of memory used by the JVM.
- Given a Java class with a main method, draw a diagram to show the state of the JVM's memory.
- Write a Java program that can cause a stack overflow exception.
- Given a diagram that shows the memory state of the JVM, mark the elements that will be removed by a garbage collection cycle.
- Given a specification for cyclic data, write a Java class that implements the specification.
- Given a set of Java classes, verify object state by writing JUnit tests.
- Given a Java class with mutable state, write pre-conditions for each method.
- Given a Java class with mutable state, write post-conditions for each method.
- Given a Java class with mutable state, write a class invariant.
- Given two Java classes, show if one class is a behavioral subtype of the other.
- DUE DATE: February 11th @ 12:00pm (NOON)
- DUE DATE: February 11th @ 12:00am (MIDNIGHT)
Problem 1
All Java source code that is part of your solution to this problem must reside inside a java package with the name
edu.neu.ccs.cs5004.seattle.assignment4.problem1
Refactor your implementations of all ADTs from Assignment 3.
Problem 2
All Java source code that is part of your solution to this problem must reside inside a java package with the name
edu.neu.ccs.cs5004.seattle.assignment4.problem2
Extend your implementation of Set to include the following operations
-
union(Set s) : Set; callings1.union(s2)wheres1s2are bothSets returns a newSetthat is the set union ofs1ands2. -
intersection(Set s) : Set; callings1.intersection(s2)wheres1s2are bothSets returns a newSetthat is the set intersection ofs1ands2. -
difference(Set s) : Set; callings1.difference(s2)wheres1s2are bothSets returns a newSetthat is the set symmetric difference ofs1ands2. -
subset(Set s) : Boolean; callings1.subset(s2)wheres1s2are bothSets returns true ifs1is a subset ofs2and false otherwise.
Problem 3
All Java source code that is part of your solution to this problem must reside inside a java package with the name
edu.neu.ccs.cs5004.seattle.assignment4.problem3
Design and implement in Java a Binary Tree (BT) whose nodes can
hold Integer objects. Your design and implementation
should support at a minimum the following
operations on a BT:
- create an empty BT
- add a new Integer in the BT. The new Integer can be added anywhere on the existing BT.
- the ability to check if the tree is the empty tree
-
the ability to return the longest path on the tree as a string, e.g,
3,5,1,2 - the ability to know if a given Integer is already in the BT
-
provide a method called
isBst()that returnstrueif a BT is a valid BST and. A BST is a BT that satifies the following conditions- For any node n in the BST all nodes in the left sub-tree contain integers that are less than the integer at n.
- For any node n in the BST all nodes in the right sub-tree contain integers that are greater than the integer at n.
-
add the operation
deleteNodeto BT; the operation takes in anInteger,n, and ifnis in the BT then removenfrom the BT and return the new BT, else ifnis not in the BT return the BT unchanged. The BT returned must be a valid BT, i.e., no dead nodes. CallingdeleteNodeon an empty BT should signal an error. -
add the operation
deleteNodeFromBST; the operation first checks that the BT is a BST. If it is not a BST then it should signal an error. If it is a BST it should delete the node provided as argument to the method and rearrange the remaining nodes as needed to to return a valid BST back. If it is a BST but the node provided as argument is not present in the BST, return the BST unchanged. -
add the operation
mirrorto BT; the operation returns a mirror image of the current BT. Here is an example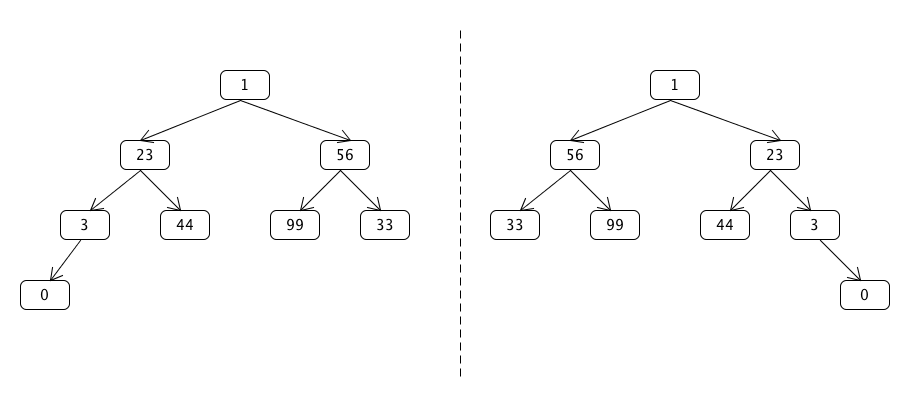
- a priority; typically an integer
- a value associated with the priority; in our case the value will be a string
-
add(Integer priority, String value) : PQ; adds the given value with its associated priority in PQ. -
peek() : String; returns the value in PQ that has the highest priority. The PQ remains unchanged. Callingpeek()on an empty PQ should signal an error. -
pop() : PQ; returns the PQ without the element with the highest priority. Callingpop()on an empty PQ should signal an error. -
isEmpty() : Boolean; returns true if the PQ is empty, returns false otherwise.
Problem 4
All Java source code that is part of your solution to this problem must reside inside a java package with the name
edu.neu.ccs.cs5004.sp15.seattle.assignment4.problem4
You are asked to implement a Priority Queue (PQ). Each element of a PQ is made up of
The PQ should have the following operations
- DUE DATE: March 2nd @ 12:00am (MIDNIGHT)
Binary Search Trees with mutation
You asked to design a program in Java to implement the following Binary Search Tree (BST) data type.
-
create() : BST- creates an empty BST -
isEmpty() : Boolean- returns true of the BST is the empty one and false otherwise -
add(Integer n) : void- adds the elementninto the BST. If the element we are trying to add is already in the BST, the BST remains unchanged. -
remove(Integer n) : void- removes the elementnfrom the BST. If the element is not present in the BST then the BST remains unchanged. -
contains(Integer n) : Boolean- returns true if the elementnis in the BST and false otherwise. -
size() : Integer- returns the total number of elements in the BST
Queue with mutation
You are asked to design a program in Java to implement the following first in, first out (FIFO) Queue data type.
-
create() : Queue- creates an empty Queue -
isEmpty() : Boolean- returns true of the Queue is the empty one and false otherwise -
enqueue(String n) : void- adds the elementninto the Queue. -
dequeue() : String- removes the oldest element from the Queue and returns it to the caller. -
remove(String n) : void- removes the elementnfrom the Queue. If the element is not in the Queue the Queue remains unchanged. After the removal of an element, the remaining elements should maintain their order, e.g., given a queue("a","b","c","d")after removing"c"the Queue's behavior should be identical to the Queue("a","b","d") -
contains(String n) : Boolean- returns true if the elementnis in the Queue and false otherwise. -
size() : Integer- returns the total number of elements in the Queue
