14 Beyond Software Development
03 October 2024
Questions?
14.1 Today
2-5mins
The course has covered material on technical ideas that you are not necessarily practiced yet in industry but are well within reach. (And some teams in some large sw companies do practice such things already.)
The rest of the semester we will practice basic “soft skills,” which again are practiced in different ways in some settings. Key is that many are also within reach when you graduate but you may have to “manage up.”
Today’s lecture goes somewhat beyond what you can easily get out there.
What do programming language researchers work on to help software engineers? The example we cover today is contracts.
14.2 Assertions
5-10mins
Defensive Programming
(provide create-equation) ... (define (create-equation lhs rhs) ; — defensive — (unless (<= 1 (length lhs) 4) (error ...)) (unless (<= 1 (length rhs) 4) (error ...)) ; — - useful code — - (eq lhs rhs))
Here is a standard example, uninteresting as code but it exemplifies everything with just a few lines:
(provide square-root) (define (square-root r) (unless (and (real? r) (>= r 0)) (error ...)) (define result 0) (let newton-s-method ([x r] ...) ... (set! result ...)) (unless (<= (- r epsilon) (* result result) (+ r epsilon)) (error ...)) result)
This is bad coding:
defensive code swamps “workhorse code”
the “Interface” does not inform client programmers of such checks
Informal pre Condition
Use English to add these constraints to the interface.
(provide ;; PRE lhs and rhs are between 1 and 4 elements long create-equation) ... (define (make-equation lhs rhs) ...)
(provide ;; a small real number epsilon ;; PRE the argument is a non-negative real number ;; POST the square of the result is within epsilon of the argument square-root) (define (square-root r) (define result 0) (let newton-s-method ([x r] ...) ... (set! result ...)) result)
14.3 Contracts
10-15mins
From Informal to Formal PRE Conditions
We want both: English and code that makes it precise.
Turn the English into code—
(provide (contract-out [create-equation (->i ([lhs (listof pebble?)] [rhs (listof pebble?)]) #:pre (lhs rhs) (and (<= 1 (length lhs) 4) (<= 1 (length rhs) 4)) any/c)])) ... (define (make-equation lhs rhs) ...)
use 5-2-contract.rkt
(provide ;; a small real number epsilon ;; PRE the argument is a non-negative real number ;; POST the square of the result is within epsilon of the argument (contract-out [square-root (->i ([a (and/c real? (>=/c 0))]) (r real?) #:post (r a) (<= (- a epsilon) (* r r) (+ a epsilon)))])) ... (define (square-root r) (define result 0) (let newton-s-method ([x r] ...) ... (set! result ...)) result)
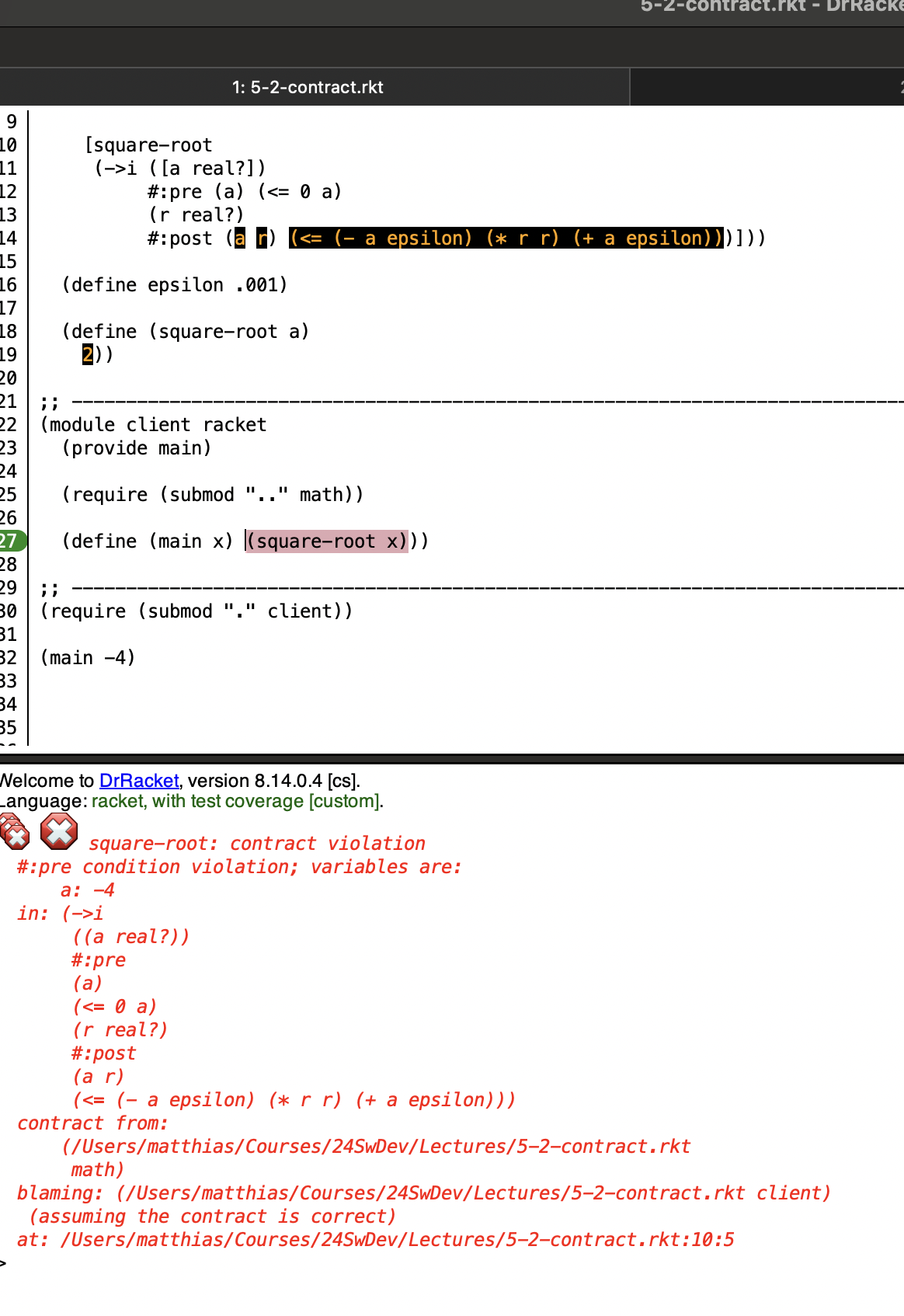
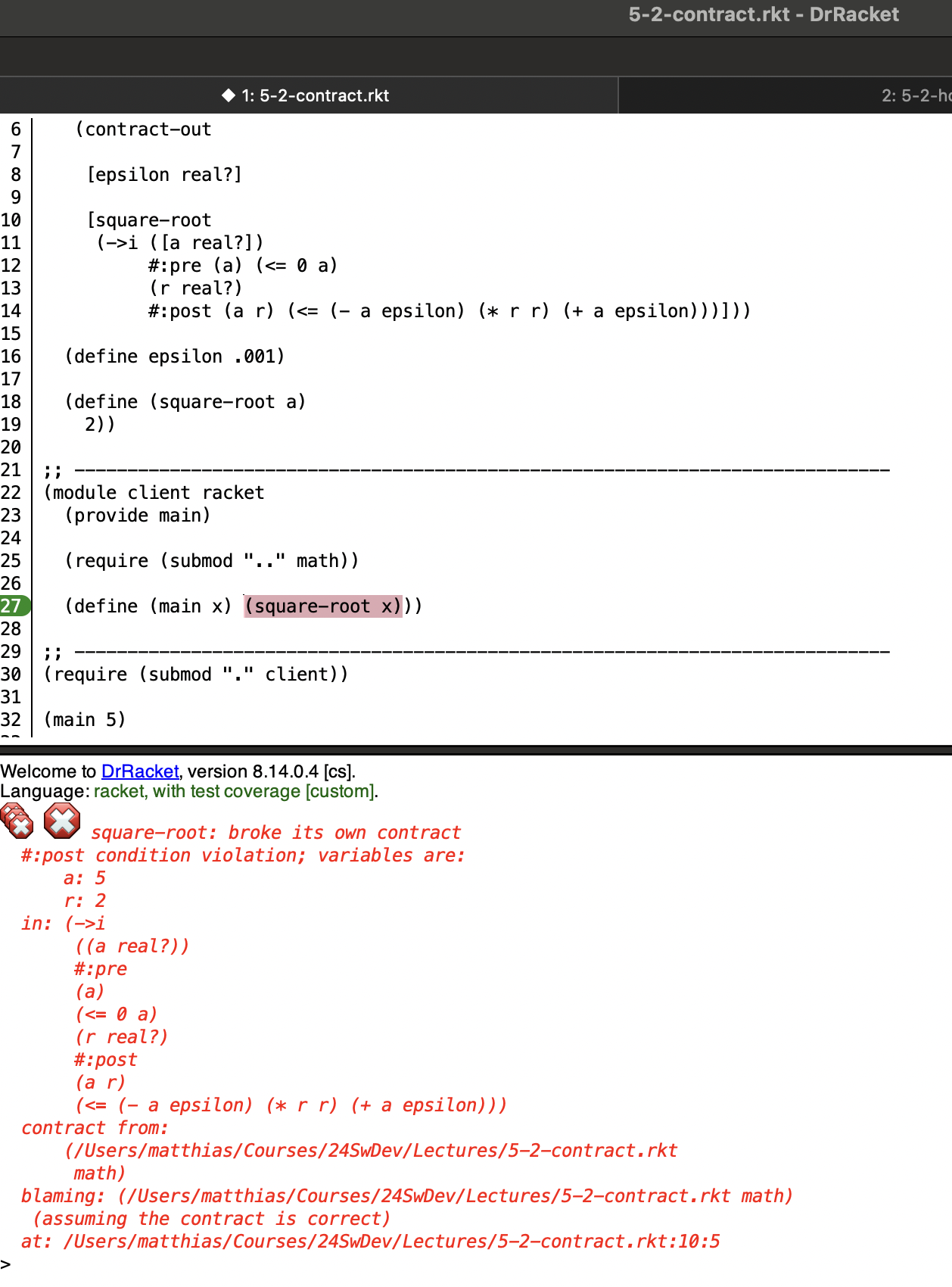
What do contracts deliver: an error message such that
if the caller doesn’t satisfy the pre-condition (obligation), it gets blamed;
if the method doesn’t satisfy the post-condition (promise), it gets blamed
Figure 3: Demo: client breaks contract
Figure 4: Demo: service breaks promise
14.4 How to do some of this in Java
10-15mins
The basic idea is simple: split the functionality into a public method and a private “workhorse” method.
The private method contains just the code that computes the result.
The public method contains just the checks that enforce the PRE (obligations) and POST (promises) conditions.
class Equation { |
// public constructor, which checks pre conditions |
public Equation(Pebbles[] lhs, Pebbles rhs[]) { |
assert(lhs.size() == FOUR); |
assert(rhs.size() == FOUR); |
Equations(lhs, rhs, true); |
} |
|
// private constructor ... |
private Equations(Pebbles[] lhs, Pebbles rhs[], boolean okay) { |
... |
} |
} |
class Math { |
public real square_root(real a) { |
assert(a >= 0); |
real r = workhorse_square_root(a); |
real c = r * r; |
assert( a - epsilon <= c && c <= a + epsilon ); |
return r; |
} |
|
private real workhorse_square_root(real a) { |
// Newton's method |
... |
} |
} |
14.5 Higher-order Contracts
15-20mins
use 5-2-ho.rkt
a module that simulates how an ATM processes a request via a credit card
"atm.rkt"
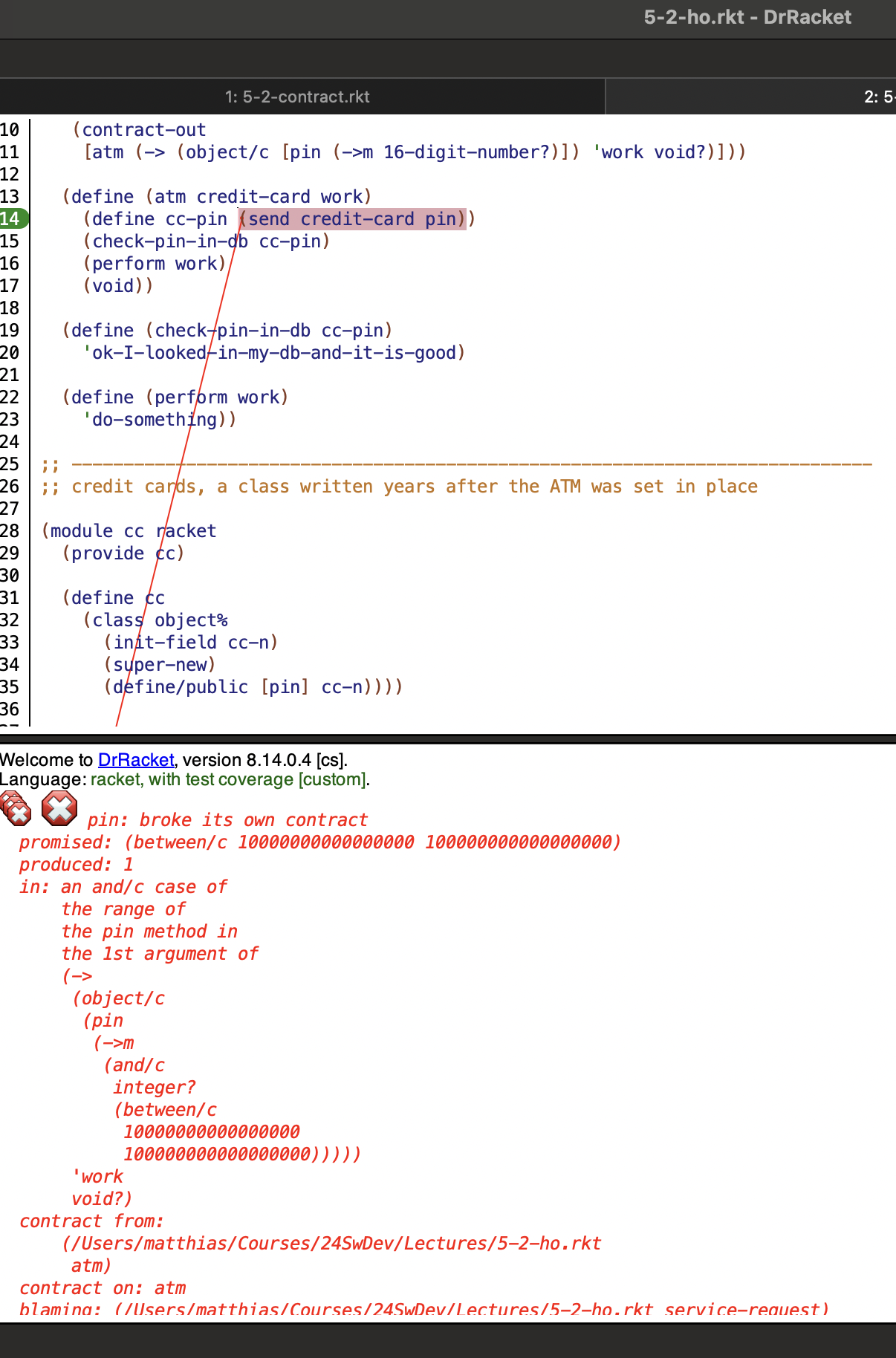
#lang racket (define 16-digits? (and/c integer? (between/c (expt 10 16) (expt 10 17)))) (provide (contract-out [atm (-> (object/c [pin (->m 16-digits?)]) 'work void?)])) ;; — — — — — — — — — — — — — — — — — — — — — — ;; implementation (define (atm credit-card work) (define cc-pin (send credit-card pin)) (check-pin-in-db cc-pin) (perform work) (void)) (define (check-pin-in-db cc-pin) 'ok-I-looked-in-my-db-and-it-is-good) (define (perform work) 'do-something)
This arrangement imposes a contract on instances of classes that have not been written. An ATM arrangement is an open system.
credit cards, a class written years after the ATM was set in place
"cc.rkt"
#lang racket (provide cc) (define cc (class object% (init-field cc-n) (super-new) (define/public [pin] cc-n)))
let’s simulate a request for service some time later still
"service-request"
#lang racket (require "atm.rkt") (require "cc.rkt") (code:commnet2 a good call) (atm (new cc [cc-n (+ (expt 10 16) 1)]) 'work) (code:commnet2 a faulty call) (atm (new cc [cc-n 1]) 'work)
Figure 5: Demo: Client breaks higher-order obligation
14.6 Stretch Goal: Trace Contracts
15-20mins
use 5-2-trace.rkt
Consider the most primitive form of a board game and how a “mechanical” player may participate:
(define player% (class object% (super-new) ; every board game needs to be set up (define/public (setup) (void)) ; almost every board game is played on a by-turn basis (define/public (take-turn s) s) ; the winner should be informed (define/public (u-re-a-winner) 'hooray)))
don’t call take-turn before setup;
don’t call take-turn concurrently for the same player;
eventually, a player’s u-re-a-winner method is called; and
don’t call any method after u-re-a-winner is called.
These constraints aren’t plain contracts of even higher-order contracts. First, they have a temporal nature. Second, the latter are about the nature of individual calls while these player constraints are about relationships across several different methods. A similar set of constraints would govern a method that promises to return ever larger integers on successive calls.
Cameron’s dissertation introduces a low-level mechanism to express and check
such constraints at run time: trace contracts. Roughly speaking, a trace
contract collects the sequence—
In principle, checking a property is just a predicate function from the stream to Boolean. But, it is also the case that constraint sets are concisely expressible via problem-specific notations. For example, one can think of the names of methods as the letters of an alphabet and then form a regular expression to state some of the constraints concerning a board-game player:
setup ; (take-turn ^*); u-re-a-winner |
Regular expressions are checked with finite-state machines and that is a well-known, easily optimized technique dating back to the 1950s.
Exercise Design a predicate good-call-sequence that consumes a list of “letters” and expresses the same property.
"board-player.rkt"
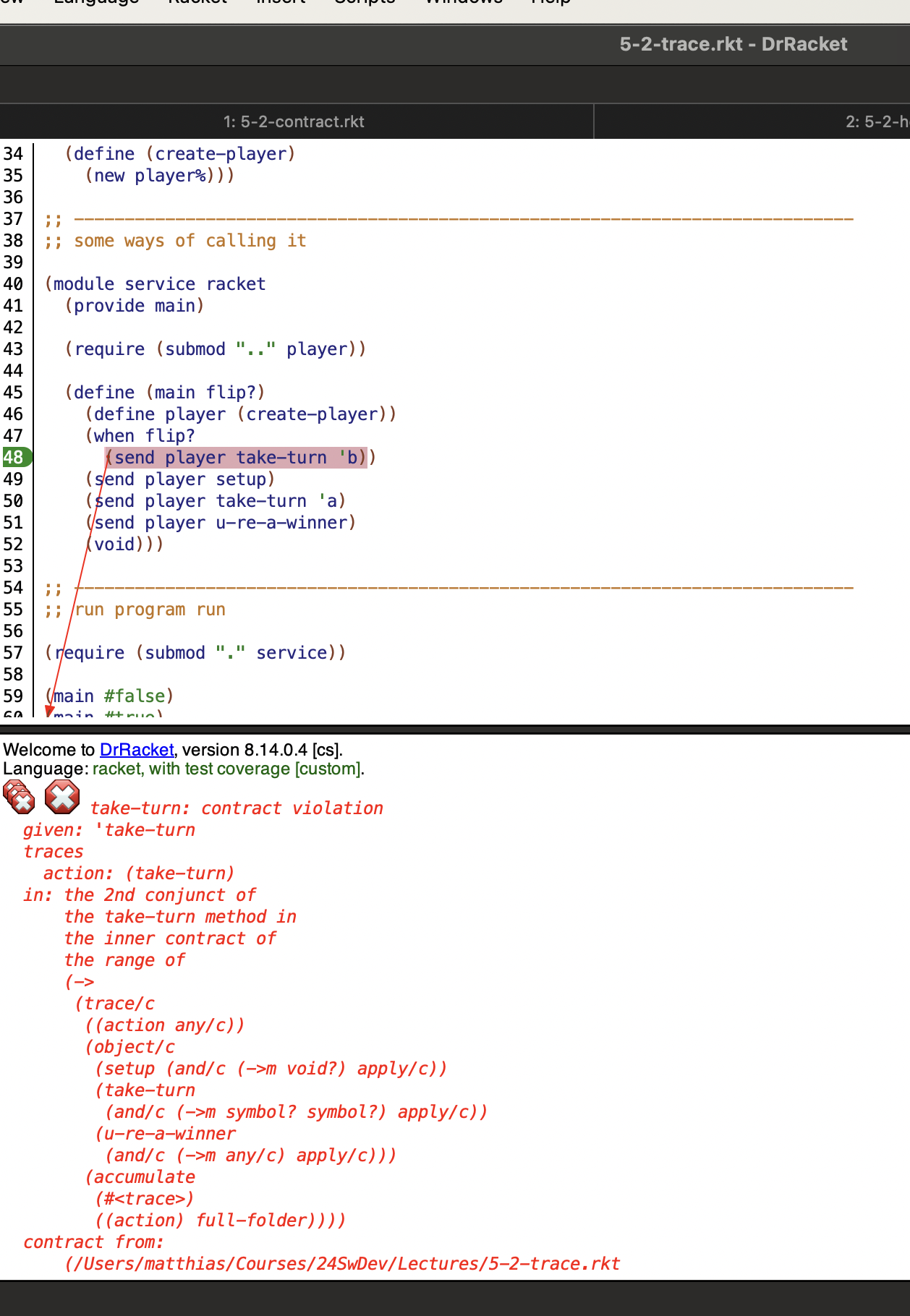
#lang racket (require trace-contract contract-etc automata/machine automata/re automata/re-ext) ; — — — — — — — — — — — — — — — — — — — — — — — — — (provide (contract-out [create-player (-> player/c)])) (define PLAYER-RE (re (seq/close 'setup (star 'take-turn) 'u-re-a-winner))) (define (okay? los) (machine-accepts? PLAYER-RE los)) (define player/c (trace/c ([action any/c]) (object/c [setup (and/c (->m void?) (apply/c [action 'setup]))] [take-turn (and/c (->m symbol? symbol?) (apply/c [action 'take-turn]))] [u-re-a-winner (and/c (->m any/c) (apply/c [action 'u-re-a-winner]))]) (full (action) okay?))) ; — — — — — — — — — — — — — — — — — — — — — — — — — (define player% (class object% (super-new) (define/public (setup) (void)) (define/public (take-turn s) s) (define/public (u-re-a-winner) 'hooray))) (define (create-player) (new player%))
Here is a simplistic client module:
"client.rkt"
#lang racket (provide main) (require "board-player.rkt") (define (main flip?) (define player (create-player)) (when flip? (send player take-turn 'b)) (send player setup) (send player take-turn 'a) (send player u-re-a-winner) (void))
Using this client module in good and bad ways still yields the “pruning” blame-assignment messages from the higher-order contract system:
(require "client.rkt") (main #false) (main #true)
Figure 6: Demo: Client breaks trace obligation
Total: 42–65 mins