14 Beyond Software Development🔗

03 October 2024

Questions?

14.1 Today🔗

2-5mins

The course has covered material on technical ideas that you are not necessarily practiced yet in industry but are well within reach. (And some teams in some large sw companies do practice such things already.)

The rest of the semester we will practice basic “soft skills,” which again are practiced in different ways in some settings. Key is that many are also within reach when you graduate but you may have to “manage up.”

Today’s lecture goes somewhat beyond what you can easily get out there.

What do programming language researchers work on to help software engineers? The example we cover today is contracts.

14.2 Assertions🔗

5-10mins

Defensive Programming

(provide create-equation)

...

(define (create-equation lhs rhs)

; — defensive —

(unless (<= 1 (length lhs) 4)

(error ...))

(unless (<= 1 (length rhs) 4)

(error ...))

; —- useful code —-

(eq lhs rhs))

Here is a standard example, uninteresting as code but it exemplifies everything with just a few lines:

(provide

square-root)

(define (square-root r)

(unless (and (real? r) (>= r 0))

(error ...))

(define result 0)

(let newton-s-method ([x r] ...)

...

(set! result ...))

(unless (<= (- r epsilon) (* result result) (+ r epsilon))

(error ...))

result)

This is bad coding:

• defensive code swamps “workhorse code”

• the “Interface” does not inform client programmers of such checks

Informal pre Condition

Use English to add these constraints to the interface.

(provide

;; PRE lhs and rhs are between 1 and 4 elements long

create-equation)

...

(define (make-equation lhs rhs)

...)

(provide

;; a small real number

epsilon

;; PRE the argument is a non-negative real number

;; POST the square of the result is within epsilon of the argument

square-root)

(define (square-root r)

(define result 0)

(let newton-s-method ([x r] ...)

...

(set! result ...))

result)

14.3 Contracts🔗

10-15mins

From Informal to Formal PRE Conditions

We want both: English and code that makes it precise.

Turn the English into code—or lift defensive code out of a method into a contract—and let the language weave these pieces of code into the function. Remove clutter. Make pre-conditions explicit.

(provide

(contract-out

[create-equation

(->i ([lhs (listof pebble?)] [rhs (listof pebble?)])

#:pre (lhs rhs) (and (<= 1 (length lhs) 4) (<= 1 (length rhs) 4))

any/c)]))

...

(define (make-equation lhs rhs)

...)

use 5-2-contract.rkt

(provide

;; a small real number

epsilon

;; PRE the argument is a non-negative real number

;; POST the square of the result is within epsilon of the argument

(contract-out

[square-root

(->i ([a (and/c real? (>=/c 0))])

(r real?)

#:post (r a) (<= (- a epsilon) (* r r) (+ a epsilon)))]))

...

(define (square-root r)

(define result 0)

(let newton-s-method ([x r] ...)

...

(set! result ...))

result)

What do contracts deliver: an error message such that

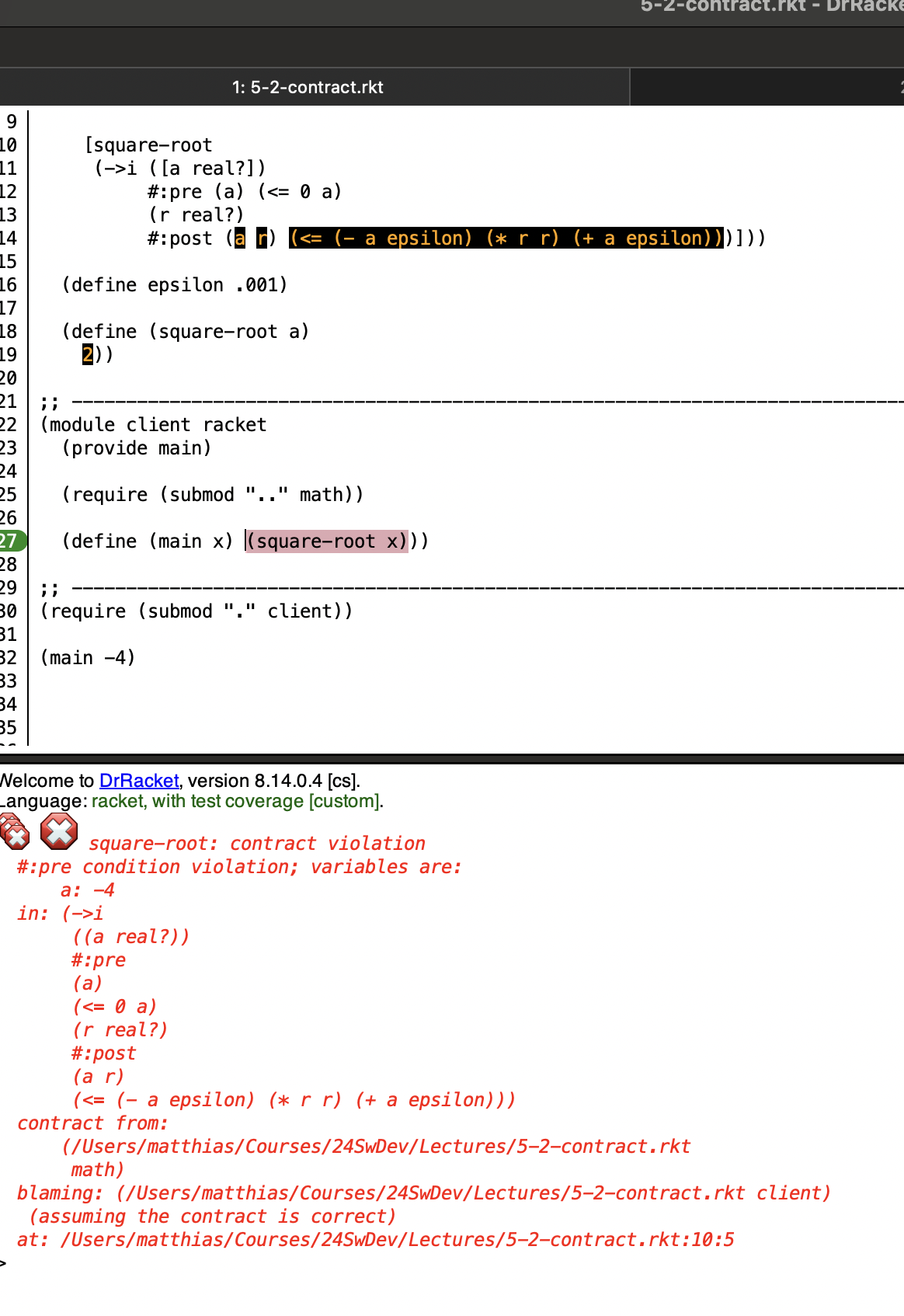
• if the caller doesn’t satisfy the pre-condition (obligation), it gets blamed;

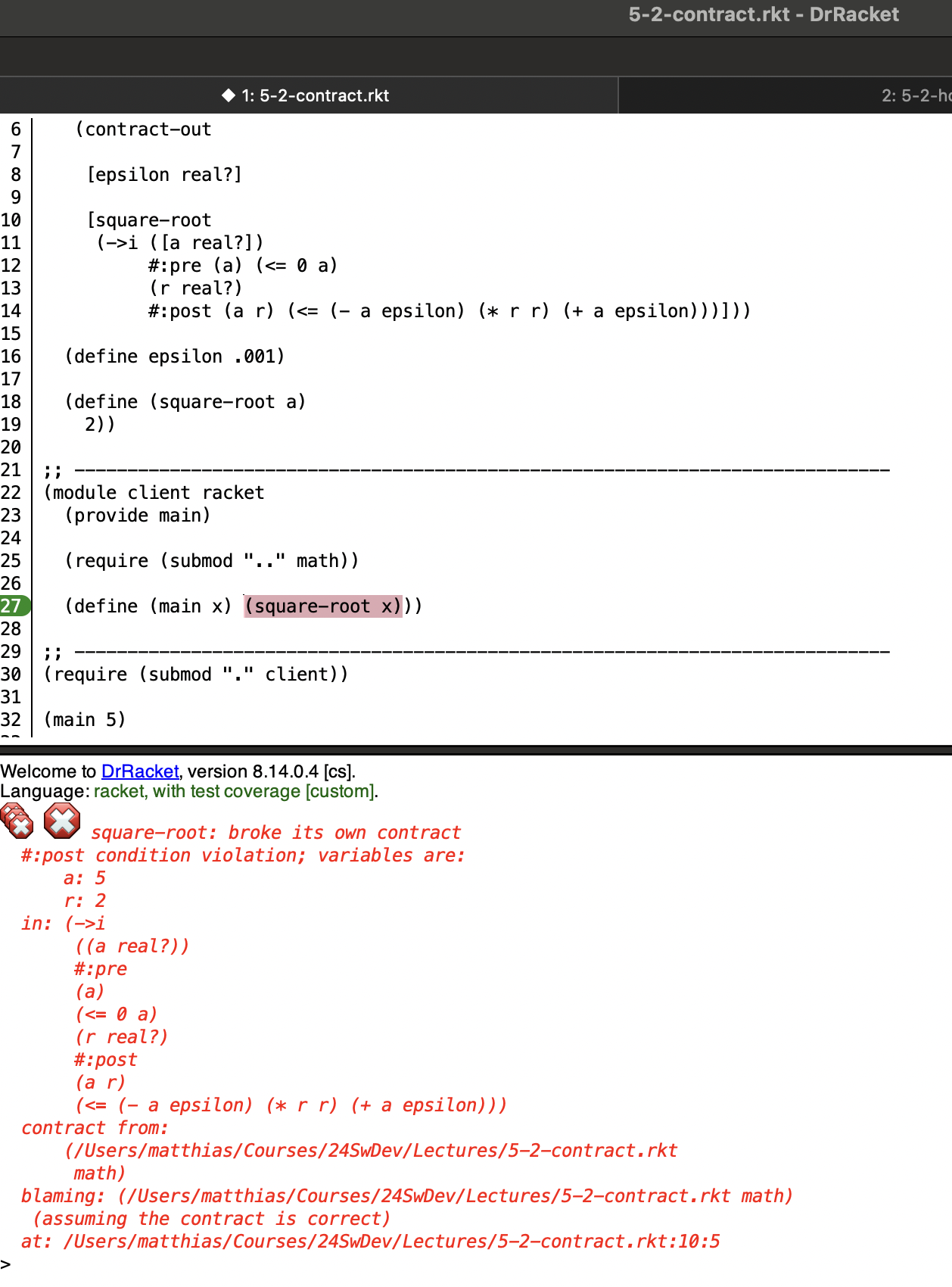
• if the method doesn’t satisfy the post-condition (promise), it gets blamed

Figure 3: Demo: client breaks contract

Figure 4: Demo: service breaks promise

14.4 How to do some of this in Java🔗

10-15mins

The basic idea is simple: split the functionality into a public method and a private “workhorse” method.

The private method contains just the code that computes the result.

The public method contains just the checks that enforce the PRE (obligations) and POST (promises) conditions.

14.5 Higher-order Contracts🔗

15-20mins

use 5-2-ho.rkt

a module that simulates how an ATM processes a request via a credit card

"atm.rkt"

#lang racket

(define 16-digits?

(and/c integer? (between/c (expt 10 16) (expt 10 17))))

(provide

(contract-out

[atm (-> (object/c [pin (->m 16-digits?)]) 'work void?)]))

;; ——————————————————————

;; implementation

(define (atm credit-card work)

(define cc-pin (send credit-card pin))

(check-pin-in-db cc-pin)

(perform work)

(void))

(define (check-pin-in-db cc-pin)

'ok-I-looked-in-my-db-and-it-is-good)

(define (perform work)

'do-something)

This arrangement imposes a contract on instances of classes that have not been written. An ATM arrangement is an open system.

credit cards, a class written years after the ATM was set in place

"cc.rkt"

#lang racket

(provide cc)

(define cc

(class object%

(init-field cc-n)

(super-new)

(define/public [pin] cc-n)))

let’s simulate a request for service some time later still

"service-request"

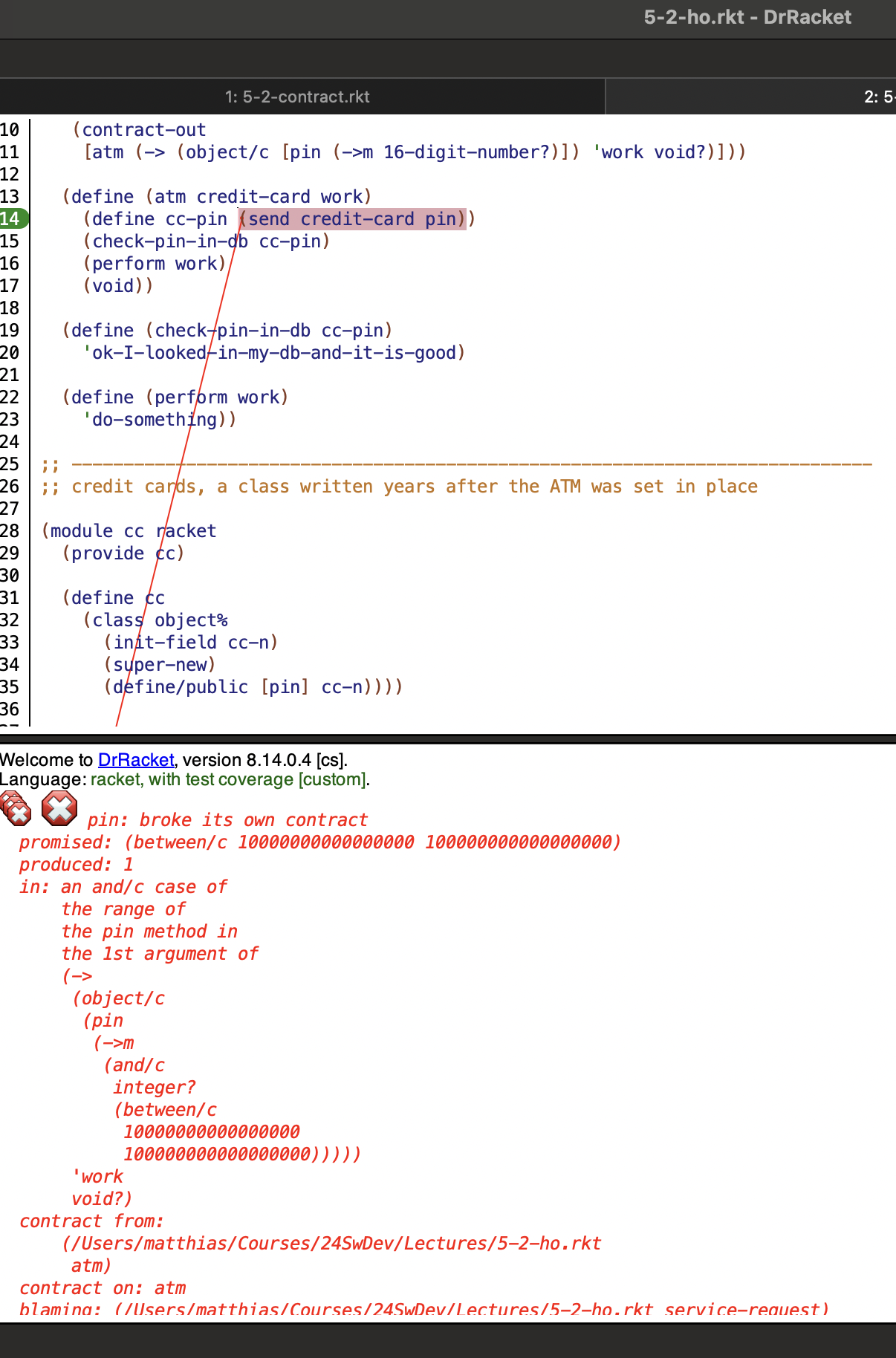
#lang racket

(require "atm.rkt")

(require "cc.rkt")

(code:commnet2 a good call)

(atm (new cc [cc-n (+ (expt 10 16) 1)]) 'work)

(code:commnet2 a faulty call)

(atm (new cc [cc-n 1]) 'work)

Figure 5: Demo: Client breaks higher-order obligation

14.6 Stretch Goal: Trace Contracts🔗

15-20mins

use 5-2-trace.rkt

Consider the most primitive form of a board game and how a “mechanical” player may participate:

(define player%

(class object%

(super-new)

; every board game needs to be set up

(define/public (setup) (void))

; almost every board game is played on a by-turn basis

(define/public (take-turn s) s)

; the winner should be informed

(define/public (u-re-a-winner) 'hooray)))

These constraints aren’t plain contracts of even higher-order contracts. First, they have a temporal nature. Second, the latter are about the nature of individual calls while these player constraints are about relationships across several different methods. A similar set of constraints would govern a method that promises to return ever larger integers on successive calls.

Cameron’s dissertation introduces a low-level mechanism to express and check such constraints at run time: trace contracts. Roughly speaking, a trace contract collects the sequence—aka trace—of values that flow through certain points in a stream and checks properties of this stream every time it is extended.

In principle, checking a property is just a predicate function from the stream to Boolean. But, it is also the case that constraint sets are concisely expressible via problem-specific notations. For example, one can think of the names of methods as the letters of an alphabet and then form a regular expression to state some of the constraints concerning a board-game player:

Regular expressions are checked with finite-state machines and that is a well-known, easily optimized technique dating back to the 1950s.

Exercise Design a predicate good-call-sequence that consumes a list of “letters” and expresses the same property.

Here is a simplistic client module:

"client.rkt"

#lang racket

(provide main)

(require "board-player.rkt")

(define (main flip?)

(define player (create-player))

(when flip?

(send player take-turn 'b))

(send player setup)

(send player take-turn 'a)

(send player u-re-a-winner)

(void))

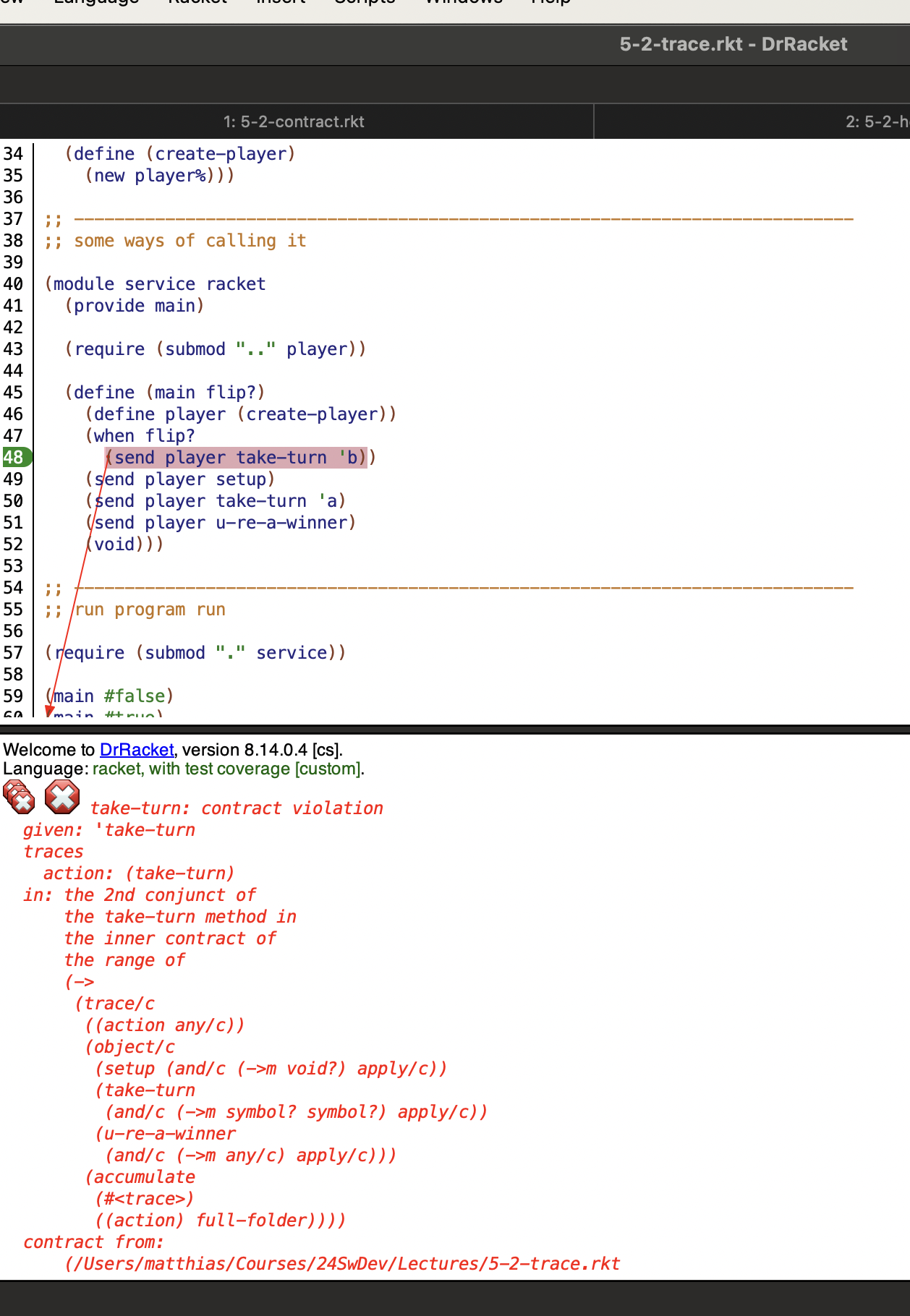
Using this client module in good and bad ways still yields the “pruning” blame-assignment messages from the higher-order contract system:

(require "client.rkt")

(main #false)

(main #true)

Figure 6: Demo: Client breaks trace obligation

Total: 42–65 mins