Machine Learning

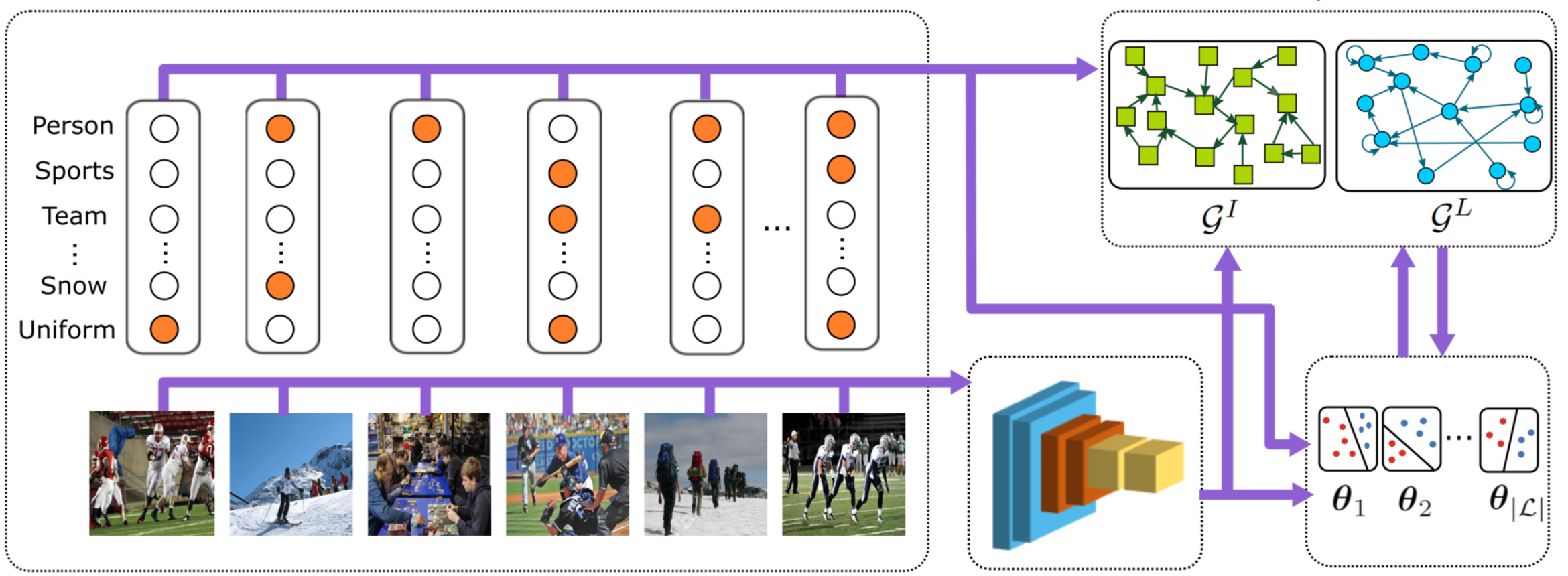
Structured Subset Selection in Sequential Multimodal Data One of the fundamental challenges across different areas of science and engineering is the massive amounts of data that need to be processed. Subset selection addresses this challenge by finding a small subset of representative data from a large dataset. This project develops a mathematical framework for subset selection in sequential data, including time-series and ordered data, that incorporates dynamic models and dependencies among data and handles multimodal data. We use techniques based on convex and non-convex optimization, including submodular maximization and sparse recovery to develop algorithms and analyze their theoretical guarantees. We apply these algorithms to solve challenging computer vision problems, including procedure learning and video summarization.

Weakly Supervised Multilabel Learning Algorithms Recognition of all present concepts in a sample, such as an image or a video, referred to as multilabel learning, is a fundamental machine learning problem with a wide range of applications, including self-driving cars, surveillance systems and assistive robots. In this project, we address the problem of multilabel recognition of a large number of labels using deep neural networks in the presence of limited number of annotated samples per label. We bring semi-supervised learning to multilabel recognition, address limitations of each class of these methods and develop robust and scalable frameworks that handle noise in labels and have linear complexity in the size of the data.

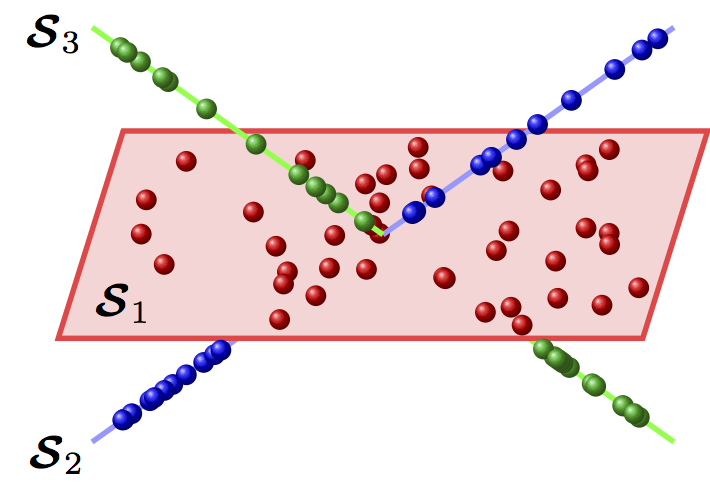Sparse Subspace Clustering and Completion Sparse Subspace Clustering (SSC) is a method based on parsimonious modeling for clustering a collection of high-dimensional data lying in a union of low-dimensional subspaces. SSC finds a sparse representation of each data point in the dictionary of the data itself to form a similarity graph from which we obtain clustering by partitioning the graph. In this project, we develop algorithms and theory for clustering, completion and error correction in high-dimensional multi-manifold data by extending SSC. We apply our methods to problems in computer vision and robotics, including motion segmentation and object/activity clustering.

Active Learning In many classification problems, we have access to a large number of samples, however, obtaining labels for samples is often hard, expensive and time consuming. Active learning methods progressively select and annotate most informative unlabeled samples to maximize the classifier’s performance. In this project, we develop efficient active learning algorithms, which can select multiple diverse samples according to data distribution, can work with any type of classifiers and can deal with static and dynamic datasets. We work on the application of these tools in computer vision and energy systems.

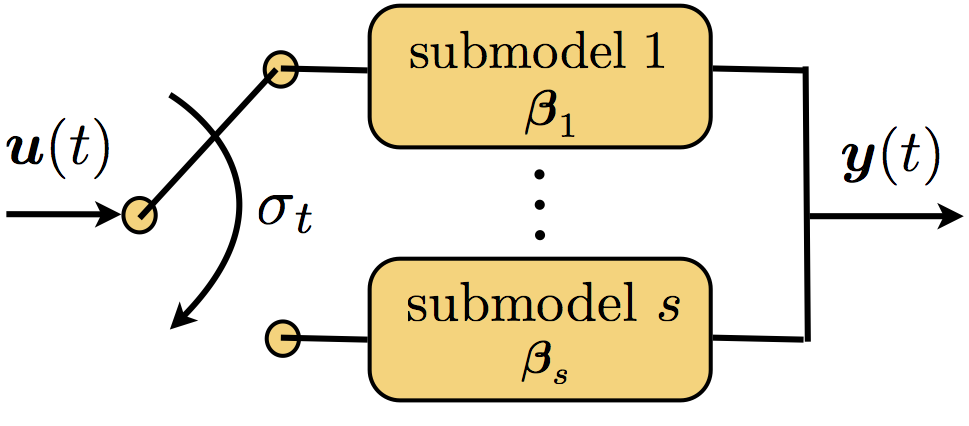Learning Nonlinear Dynamic Models We consider the problem of modeling and segmentation of time-series data generated by switching among dynamical systems. This problem finds applications in the study of human activities from videos and motion capture data, complex motor control systems, energy signals and more. We develop robust algorithms based on convex programming for segmentation and learning dynamics of such datasets. We use these tools for identification, synthesis and controls in computer vision, robotics and energy systems.

Computer Vision

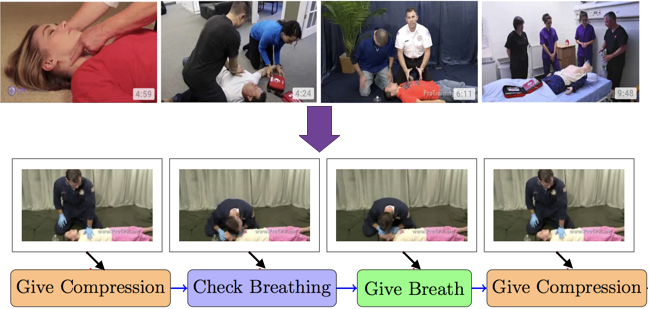Procedure Learning from Instructional Videos Learning from instructions is at the heart of many practical and important problems, including imitation learning in robotics and complex activity recognition. In this project, we address the problem of learning grammar of complex tasks using a collection of unconstrained instructional videos. We develop methods based on structured subset selection that produce a compact summary of the procedure steps and their ordering needed to perform a complex task, as well as localization of the procedure steps in videos.

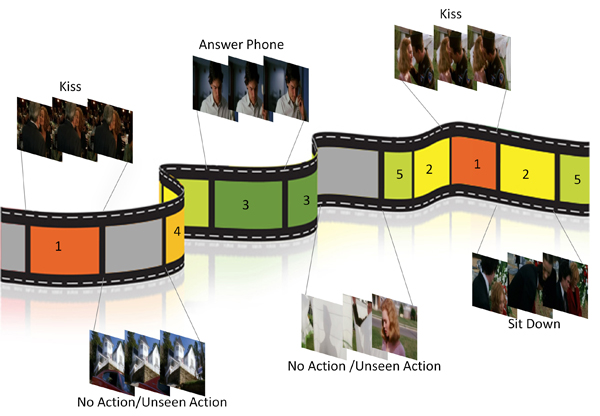Structured Video Summarization The widespread availability and low-cost of video recording devices has resulted in billions of hours of unstructured and unedited videos. In this project, we develop video summarization methods that can take hours of video footage and produce a structured summary that captures main events and relationships among these key events. We use tools from convex and submodular optimization and online learning methods to develop these methods. We apply these algorithms to real consumer videos.

Motion Segmentation in Dynamic Scenes In many problems in computer vision, a sequence of images contain objects with different motions. A fundamental step to analyze the content and build a 3D model of the scene is to segment features extracted from images according to their motions. In this project, we develop methods for motion segmentation in videos by casting the problem as clustering data in a union of low-dimensional manifolds. We apply these algorithms to real-world video datasets.

Face and Activity Recognition High-dimensional visual data often lie in low-dimensional manifolds corresponding to classes they belong to. In this project, we address the problem of human activity analysis and face recognition by modeling data in each class as a low-dimensional manifold. We develop methods based on group-sparse representation theory for classification and investigate their theoretical guarantees. We apply these algorithms to real-world images of faces, videos of human activities and motion capture data.

Optimization

Sparse and Low-Rank Recovery in Low-Dimensional Models High-dimensional data can often be represented using few atoms of an appropriate dictionary. Building such dictionaries and recovering sparse representations find important applications in a variety of problems such as clustering, classification, denoising, detection and compression. In this project, we develop algorithms for recovering sparse and low-rank representations in underdetermined dictionaries whose atoms correspond to data lying in a union of low-dimensional subspaces. We study, analyze and implement robust and efficient algorithms based on convex programming, greedy pursuit and methods informed by probabilistic graphical model inference to recover desired sparse representations.

Submodular Maximization of Structured Data Maximization of submodular set functions arises in a large number of problems, including data summarization, influence maximization, viral marketing and sensor placement. In this project, we develop and study efficient and scalable maximization of (approximately) submodular functions for structured problems in which data points are dependent. We apply our methods to problems in computer vision, including procedure learning and structured video summarization.

Disaggregation Given the growing demand for energy and limits of our resources, it is imperative to design methods that help to save energy. An important problem in this direction is disaggregation, i.e., decomposing whole energy signal into its component appliances. In this project, we develop supervised and semi-supervised algorithms for energy disaggregation. In the learning stage, we extract consumption patterns of devices, which we call ‘powerlets’ and in the inference stage, we employ integer and convex programming to disaggregate a new signal in the ‘powerlets’ dictionary. We run these methods on real energy datasets collected from consumers.