CS6140 Machine Learning
HW1 Decision Tree, Linear Regression
Make sure you check the syllabus for the due date. Please
use the notations adopted in class, even if the problem is stated
in the book using a different notation.
We are not looking for very long answers (if you find yourself
writing more than one or two pages of typed text per problem, you
are probably on the wrong track). Try to be concise; also keep in
mind that good ideas and explanations matter more than exact
details.
DATASET 1: Housing data, training and testing sets (description). The last
column are the labels.
DATATSET 2: Spambase
dataset available from the UCI Machine
Learning Repository.
You can try to normalize each column (feature) separately with
wither one of the following ideas. Do not normalize labels.
- Shift-and-scale normalization: substract the minimum, then
divide by new maximum. Now all values are between 0-1
- Zero mean, unit variance : substract the mean, divide by the
appropriate value to get variance=1.
- When normalizing a column (feature), make sure to normalize
its values across all datapoints (train,test,validation, etc)
The Housing dataset comes with predefined training and testing
sets. For the Spambase dataset use K-fold cross-validation :
- split into K folds
- run your algorithm K times each time training on K-1 of them
and testing on the remaining one
- average the error across the K runs.
PROBLEM 1 [50 points]
Using each dataset, build a decision tree (or regression tree)
from the training set. Since the features are numeric values, you
will need to use thresholds mechanisms. Report (txt or pdf file)
for each dataset the training and testing error for each of your
trials:
- simple decision tree using something like Information Gain or
other Entropy-like notion of randomness
- regression tree
- try to limit the size of the tree to get comparable training
and testing errors (avoid overfitting typical of deep trees)
PROBLEM 2 [50 points]
Using each of the two datasets above, apply regression on the
training set to find a linear fit with the labels. Implement
linear algebra exact solution (normal equations).
- Compare the training and testing errors (mean sum of square
differences between prediction and actual label).
- Compare with the decision tree results
PROBLEM 3 [20 points]
DHS chapter8, Pb1. Given an arbitrary decision tree, it might have
repeated queries splits (feature f, threshold t) on some paths
root-leaf. Prove that there exists an equivalent decision tree only
with distinct splits on each path.
[GR ONLY] DHS chapter8
a) Prove that for any arbitrary tree, with possible unequal
branching ratios throughout, there exists a binary tree that
implements the same classification functionality.
b)
Consider a tree with just two levels - a root node
connected to B leaf nodes (B>=2) . What are then upper
and the lower limits on the number of levels in a functionally
equivalent binary tree, as a function of B?
c) As in b), what are the upper and lower
limits on number of nodes in a functionally equivalent binary
tree?
PROBLEM 4 [20 points]
DHS chapter8,
Consider a binary decision tree using entropy splits.
a) Prove that the decrease in entropy by a split
on a binary yes/no feature can never be greater than 1 bit.
b) [GR-ONLY] Generalize this result to the case
of arbitrary branching B>1.
PROBLEM 5 [20 points]
Derive explicit formulas for normal equations solution
presented in class for the case of one input dimension.
(Essentially assume the data is (x_i,y_i) i=1,2,..., m and you
are looking for h(x) = ax+b that realizes the minimum mean square
error. The problem asks you to write down explicit formulas for a
and b.)
HINT: Do not simply copy the formulas from here
(but do read the article): either take the general formula derived
in class and make the calculations (inverse, multiplications,
transpose) for one dimension or derive the formulas for a and b
from scratch; in either case show the derivations. You can compare
your end formulas with the ones linked above.
PROBLEM 6 [Optional, no credit; read DHS ch5]
DHS chapter5
A classifier is said to be a piecewise linear machine if its
discriminant functions have the form
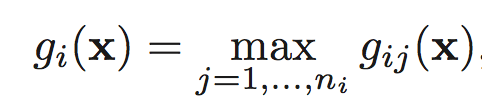
where
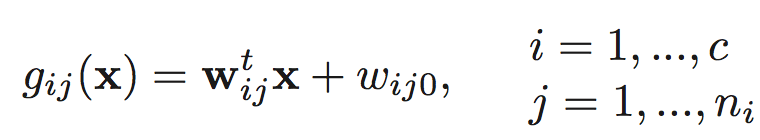
(a) Indicate how a piecewise linear machine can be viewed in terms
of a linear machine for classifying subclasses of patterns.
(b) Show that the decision regions of a piecewise linear machine can
be non convex and even multiply connected.
(c) Sketch a plot of gij(x) for a one-dimensional example in which
n1 = 2 and n2 = 1 to illustrate your answer to part (b)
PROBLEM 7 [GR ONLY]
DHS chapter5,
The convex hull of a set of vectors xi,i = 1,...,n is the set of all
vectors of the form
where the coefficients αi are nonnegative and sum to one. Given two
sets of vectors, show that either they are linearly separable or
their convex hulls intersect.
Hint on easy part: that the two conditions cannot happen
simultaneously. Suppose that both statements are true, and consider
the classification of a point in the intersection of the convex
hulls.
[Optional, no credit; difficult] Hard part: that at least one of the two
conditions must hold. Suppose that the convex hulls dont intersect;
then show the points are linearly separable.
PROBLEM 8 [Optional, no credit]
With the notation used in class (and notes), prove that
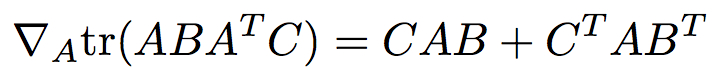
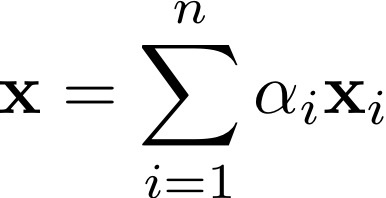
![]()