 |
 |
Andrei Broder1, Ravi
Kumar2, Farzin Maghoul1,
Prabhakar Raghavan2, Sridhar Rajagopalan2,
Raymie Stata3, Andrew Tomkins2,
Janet Wiener3
The study of the web as a graph is not only fascinating in its own right, but also yields valuable insight into web algorithms for crawling, searching and community discovery, and the sociological phenomena which characterize its evolution. We report on experiments on local and global properties of the web graph using two Altavista crawls each with over 200M pages and 1.5 billion links. Our study indicates that the macroscopic structure of the web is considerably more intricate than suggested by earlier experiments on a smaller scale.
Keywords: graph structure, diameter, web measurement
The power law for indegree: the probability that a node has in-degree i is proportional to 1/ix, for some positive x > 1.We verify the power law phenomenon in current (considerably larger) web crawls, confirming it as a basic web property.
In other recent work, [Albert, Jeong, and Barabasi 99] report the intriguing finding that most pairs of pages on the web are separated by a handful of links, almost always under 20, and suggest that this number will grow logarithmically with the size of the web. This is viewed by some as a "small world" phenomenon. Our experimental evidence reveals a rather more detailed and subtle picture: significant portions of the web cannot at all be reached from other (significant) portions of the web, and there is significant number of pairs that can be bridged, but only using paths going through hundreds of intermediate pages.
Our analysis reveals an interesting picture (Figure 9) of the web's macroscopic structure. Most (over 90%) of the approximately 203 million nodes in our crawl form a single connected component if hyperlinks are treated as undirected edges. This connected web breaks naturally into four pieces. The first piece is a central core, all of whose pages can reach one another along directed hyperlinks -- this "giant strongly connected component" (SCC) is at the heart of the web. The second and third pieces are called IN and OUT. IN consists of pages that can reach the SCC, but cannot be reached from it - possibly new sites that people have not yet discovered and linked to. OUT consists of pages that are accessible from the SCC, but do not link back to it, such as corporate websites that contain only internal links. Finally, the TENDRILS contain pages that cannot reach the SCC, and cannot be reached from the SCC. Perhaps the most surprising fact is that the size of the SCC is relatively small -- it comprises about 56M pages. Each of the other three sets contain about 44M pages -- thus, all four sets have roughly the same size.
We show that the diameter of the central core (SCC) is at least 28, and that the diameter of the graph as a whole is over 500 (see below for definitions of diameter). We show that for randomly chosen source and destination pages, the probability that any path exists from the source to the destination is only 24%. We also show that, if a directed path exists, its average length will be about 16. Likewise, if an undirected path exists (i.e., links can be followed forwards or backwards), its average length will be about 6. These analyses appear in the section on interpreting our experiments. These results are remarkably consistent across two different, large AltaVista crawls. This suggests that our results are relatively insensitive to the particular crawl we use, provided it is large enough. We will say more about crawl effects under Other Observations.
In a sense the web is much like a complicated organism, in which the local structure in a microscopic scale looks very regular like a biological cell, but the global structure exhibits interesting morphological structure (body and limbs) that are not obviously evident in the local structure. Therefore, while it might be tempting to draw conclusions about the structure of the web graph from a local picture of it, such conclusions may be misleading.
Zipf-Pareto-Yule and Power laws. Distributions with an inverse polynomial tail have been observed in a number of contexts. The earliest observations are due to Pareto [Pareto 1897] in the context of economic models. Subsequently, these statistical behaviors have been observed in the context of literary vocabulary [Yule 44], sociological models [Zipf 49], and even oligonucleotide sequences [Martindale and Konopka 96] among others. Our focus is on the closely related power law distributions, defined on the positive integers, with the probability of the value i being proportional to 1/ik for a small positive number k. Perhaps the first rigorous effort to define and analyze a model for power law distributions is due to Herbert Simon [Simon 55].
More recently, power law distributions have been observed in various aspects of the web. Two lines of work are of particular interest to us. First, power laws have been found to characterize user behavior on the web in two related but dual forms:
There is no evidence that users' browsing behavior, access statistics and the linkage statistics on the web graph are related in any fundamental way, although it is very tempting to conjecture that this is indeed the case. It is usually the case, though not always so, that pages with high in-degree will also have high PageRank [Brin and Page 98]. Indeed, one way of viewing PageRank is that it puts a number on how easy (or difficult) it is to find particular pages by a browsing-like activity. Consequently, it is plausible that the in-degree distributions induce a similar distribution on browsing activity and consequently, on access statistics.
Faloutsos, Faloutsos, and Faloutsos 99 observe Zipf/Pareto distributions (power law distributions on the ranks of values) on the internet network topology using a graph of the network obtained from the routing tables of a backbone BGP router.
Graph theoretic methods. Much recent work has addressed the web as a graph and applied algorithmic methods from graph theory in addressing a slew of search, retrieval, and mining problems on the web. The efficacy of these methods was already evident even in early local expansion techniques [Butafogo and Schneiderman 91]. Since then, the increasing sophistication of the techniques used, the incorporation of graph theoretical methods with both classical and new methods which examine context and content, and richer browsing paradigms have enhanced and validated the study and use of such methods. Following Butafogo and Schneiderman, the view that connected and strongly connected components represent meaningful entities has become accepted. [Pirolli, Pitkow and Rao 96] augment graph theoretic analysis to include document content, as well as usage statistics, resulting in a rich understanding of domain structure and a taxonomy of roles played by web pages..
Graph theoretic methods have been used for search [Kleinberg 97, Brin and Page 98, Chakrabarti et. al. (1) 98, Chakrabarti et. al. (2) 98, Bharat and Henzinger 98], browsing and information foraging [Butafogo and Schniederman 91, Pirolli, Pitkow, and Rao 96, Carierre and Kazman 97, Pitkow and Pirolli 97, Chakrabarti, Gibson, and McCurley 99], and web mining [Mendelzon and Wood 95, Mendelzon, Mihaila and Milo 97, Kumar et. al. (1) 99, Kumar et.al. (2) 99]. We expect that a better structural characterization of the web will have much to say in each of these contexts.
In this section we formalize our view of the web as a graph; in this view we ignore the text and other content in pages, focusing instead on the links between pages. Adopting the terminology of graph theory [Harary], we refer to pages as nodes, and to links as arcs. In this framework, the web becomes a large graph containing several hundred million nodes, and a few billion arcs. We will refer to this graph as the web graph, and our goal in this paper is to understand some of its properties. Before presenting our model for web-like graphs, we begin with a brief primer on graph theory, and a discussion of graph models in general.
A directed graph consists of a set of nodes, denoted V and a set of arcs, denoted E. Each arc is an ordered pair of nodes (u,v) representing a directed connection from u to v. The out-degree of a node u is the number of distinct arcs (u,v1)...(u,vk) (i.e., the number of links from u), and the in-degree is the number of distinct arcs (v1,u)...(vk,u) (i.e., the number of links to u). A path from node u to node v is a sequence of arcs (u,u1), (u1,u2), ... (uk,v). One can follow such a sequence of arcs to "walk" through the graph from u to v. Note that a path from u to v does not imply a path from v to u. The distance from u to v is one more than the smallest k for which such a path exists. If no path exists, the distance from u to v is defined to be infinity. If (u,v) is an arc, then the distance from u to v is 1.
Given a directed graph, a strongly connected component (strong component for brevity) of this graph is a set of nodes such that for any pair of nodes u and v in the set there is a path from u to v. In general, a directed graph may have one or many strong components. The strong components of a graph consist of disjoint sets of nodes. One focus of our studies will be in understanding the distribution of the sizes of strong components on the web graph.
An undirected graph consists of a set of nodes and a set of edges, each of which is an unordered pair {u,v} of nodes. In our context, we say there is an edge between u and v if there is a hyperlink between u and v, without regard to whether the link points from u to v or the other way around. The degree of a node u is the number of edges incident to u. A path is defined as for directed graphs, except that now the existence of a path from u to v implies a path from v to u. A component of an undirected graph is a set of nodes such that for any pair of nodes u and v in the set there is a path from u to v. We refer to the components of the undirected graph obtained from a directed graph by ignoring the directions of its arcs as the weak components of the directed graph. Thus two nodes on the web may be in the same weak component even though there is no directed path between them (consider, for instance, a node u that points to two other nodes v and w; thenv and w are in the same weak component even though there may be no sequence of links leading from v to w or vice versa). The interplay of strong and weak components on the (directed) web graph turns out to reveal some unexpected properties of the web's connectivity.
A breadth-first search (BFS) on a directed graph begins at a node u of the graph, and proceeds to build up the set of nodes reachable from u in a series of layers. Layer 1 consists of all nodes that are pointed to by an arc from u. Layer k consists of all nodes to which there is an arc from some vertex in layer k-1, but are not in any earlier layer. Notice that by definition, layers are disjoint. The distance of any node from u can be read out of the breadth-first search. The shortest path from u to v is the index of the layer v belongs in -- if there is such a layer. On the other hand, note that a node that cannot be reached from u does not belong in any layer, and thus we define the distance to be infinity. A BFS on an undirected graph is defined analogously.
Finally, we must take a moment to describe the
exact notions of diameter we study, since several have been discussed informally
in the context of the web. Traditionally, the diameter of
a graph, directed or undirected, is the maximum over all ordered pairs
(u,v)
of the shortest path from u to v. Some researchers
have proposed studying the average distance of a graph, defined
to be the length of the shortest path from u to v, averaged
over all ordered pairs (u,v); this is referred to as diameter in
[Albert, Jeong, and Barabasi 99].
The difficulty with this notion is that even a single pair (u,v)
with no path from u to v results in an infinite average distance.
In fact, as we show from our experiments below, the web is rife with such
pairs (thus is it is not merely a matter of discarding a few outliers before
taking this average). This motivates the following revised definition:
let P be the set of all ordered pairs (u,v) such that there is a
path from u to v. The average connected distance
is the expected length of the shortest path, where the expectation is over
uniform choices from P.
CS2 improves on the original connectivity server (CS1) described in [Bharat et.al. 98] in two important ways. First, it significantly increases the compression of the URLs and the links data structures. In CS1, each compressed URL is, on average, 16 bytes. In CS2, each URL is stored in 10 bytes. In CS1, each link requires 8 bytes to store as both an in-link and out-link; in CS2, an average of only 3.4 bytes are used. Second, CS2 provides additional functionality in the form of a host database. For example, in CS2, it is easy to get all the in-links for a given node, or just the in-links from remote hosts.
Like CS1, CS2 is designed to give high-performance access to all this data on a high-end machine with enough RAM to store the database in memory. On a 465 MHz Compaq AlphaServer 4100 with 12GB of RAM, it takes 70-80 ms to convert a URL into an internal id or vice versa, and then only 0.15 ms/link to retrieve each in-link or out-link. On a uniprocessor machine, a BFS that reaches 100M nodes takes about 4 minutes; on a 2-processor machine we were able complete a BFS every two minutes.
In the experiments reported in this paper, CS2 was built from a crawl performed at AltaVista in May, 1999. The CS2 database contains 203 million URLs and 1466 million links (all of which fit in 9.5 GB of storage). Some of our experiments were repeated on a more recent crawl (October, 1999) containing 271 million URLs and 2130 million links.
In general, the AltaVista crawl is based on a large set of starting points accumulated over time from various sources, including voluntary submissions. The crawl proceeds in roughly a BFS manner, but is subject to various rules designed to avoid overloading web servers, avoid robot traps (artificial infinite paths), avoid and/or detect spam (page flooding), deal with connection time outs, etc. Each build of the AltaVista index is based on the crawl data after further filtering and processing designed to remove duplicates and near duplicates, eliminate spam pages, etc. Then the index evolves continuously as various processes delete dead links, add new pages, update pages, etc. The secondary filtering and the later deletions and additions are not reflected in the connectivity server. But overall, CS2's database can be viewed as a superset of all pages stored in the index at one point in time. Note that due to the multiple starting points, it is possible for the resulting graph to have many connected components.
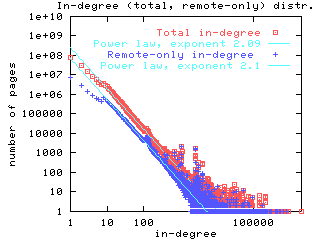
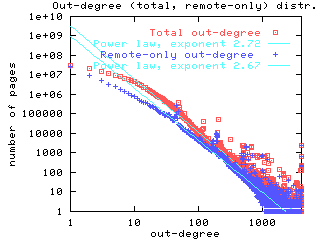
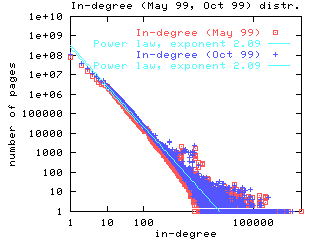
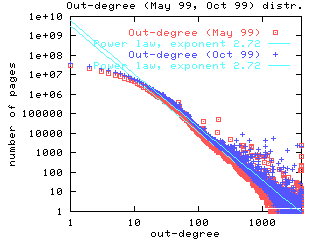
Degree sequences. The first experiment we ran was to verify earlier observations that the in- and out-degree distributions on the web are distributed according to power laws. We ran the experiment on both the May and October crawls of the web. The results, shown in Figure 1, show remarkable agreement with each other, and with similar experiments from data that is over two years old [Kumar et. al. (1) 99]. Indeed, in the case of in-degree, the exponent of the power law is consistently around 2.1, a number reported in [Kumar et. al. (1) 99,Barabasi and Albert 99]. The anomalous bump at 120 on the x-axis is due a large clique formed by a single spammer. In all our log-log plots, straight lines are linear regressions for the best power law fit.
Out-degree distributions also exhibit a power law, although the exponent
is 2.72, as can be seen in Figure 2.
It is interesting to note that the initial segment of the out-degree distribution
deviates significantly from the power law, suggesting that pages with low
out-degree follow a different (possibly Poisson or a combination of Poisson
and power law, as suggested by the concavity of the deviation) distribution.
Further research is needed to understand this combination better.
 |
 |
 |
 |
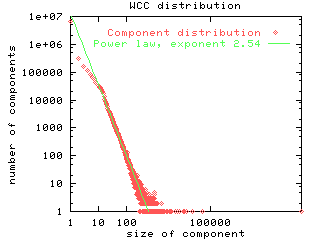
Undirected connected components. In the next set of experiments
we treat the web graph as an undirected graph and find the sizes of
the undirected components. We find a giant component of 186 million nodes
in which fully 91% of the nodes in our crawl are reachable from one another
by following either forward or backward links. This is done by running
the WCC algorithm which simply finds all connected components in the undirected
web graph. Thus, if one could browse along both forward and backward directed
links, the web is a very well connected graph. Surprisingly,
even the distribution of the sizes of WCC's exhibits a power law with exponent
roughly 2.5 (Figure 5).
 |
 |
Does this widespread connectivity result from a few nodes of large in-degree
acting as "junctions"? Surprisingly, this turns out not to be the
case. Indeed, even if all links to pages with in-degree 5 or higher
are removed (certainly including links to every well-known page on the
web), the graph still contains a giant weak component of size 59 million.
This provides us with two interesting and useful insights. First, the connectivity
of the web graph as an undirected graph is extremely resilient and does
not depend on the existence of nodes of high in-degree. Second, such nodes,
which are very useful and tend to include nodes with high PageRank or nodes
that are considered good hubs and authorities, are embedded in a graph
that is well connected without them. This last fact may help understand
why algorithms such as HITS [Kleinberg] converge
quickly.
| k | 1000 | 100 | 10 | 5 | 4 | 3 |
| Size (millions) | 177 | 167 | 105 | 59 | 41 | 15 |
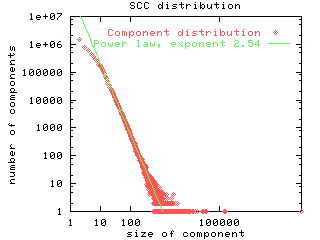
Strongly connected components. Motivated in part by the intriguing prediction of [Albert, Jeong, and Barabasi 99] that the average distance (referred to in their paper as diameter) of the web is 19 (and thus it should be possible to get from any page to any other in a small number of clicks), we turned to the strongly connected components of the web as a directed graph. By running the strongly connected component algorithm, we find that there is a single large SCC consisting of about 56M pages, all other components are significantly smaller in size. This amounts to barely 28% of all the pages in our crawl. One may now ask: where have all the other pages gone? The answer to this question reveals some fascinating detailed structure in the web graph; to expose this and to further study the issues of the diameter and average distance, we conducted a further series of experiments. Note that the distribution of the sizes of SCCs also obeys a power law (Figure 6).
Random-start BFS. We ran the BFS algorithm twice from each of 570 random sample of starting nodes: once in the forward direction, following arcs of the web graph as a browser would, and once backward following links in the reverse direction. Each of these BFS traversals (whether forward or backward) exhibited a sharp bimodal behavior: it would either "die out" after reaching a small set of nodes (90% of the time this set has fewer than 90 nodes; in extreme cases it has a few hundred thousand), or it would "explode" to cover about 100 million nodes (but never the entire 186 million). Further, for a fraction of the starting nodes, both the forward and the backward BFS runs would "explode", each covering about 100 million nodes (though not the same 100 million in the two runs). As we show below, these are the starting points that lie in the SCC.
The cumulative distributions of the nodes covered in these BFS runs
are summarized in Figure 7 -- they reveal that the
true structure of the web graph must be somewhat subtler than a "small
world" phenomenon in which a browser can pass from any web page to any
other with a few clicks. We explicate this structure in the section
below on Interpretation.
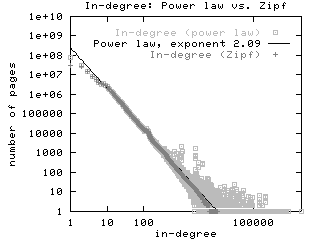
Zipf distributions vs power law distributions.
The Zipf distribution is an inverse polynomial function of ranks
rather than magnitudes -- for example, if only in-degrees 1, 4, and 5 occurred
then a power law would be inversely polynomial in those values, whereas
a Zipf distribution would be inversely polynomial in the ranks of those
values: i.e., inversely polynomial in 1, 2, and 3. The in-degree
distribution in our data shows a striking fit with a Zipf (more so than
the power law) distribution; Figure 8 shows the
in-degrees of pages from the May 1999 crawl plotted against both ranks
and magnitudes (corresponding to the Zipf and power law cases). The
plot against ranks is virtually a straight line in the log-log plot, without
the flare-out noticeable in the plot against magnitudes.
 |
|
|
We now give a more detailed description of the structure in Figure
9. The sizes of the various components are as follows:
| Region | SCC | IN | OUT | TENDRILS | DISC. | Total |
| Size | 56,463,993 | 43,343,168 | 43,166,185 | 43,797,944 | 16,777,756 | 203,549,046 |
These sizes were determined as follows. We know the total number of nodes in our crawl, so by subtracting the size of the giant weak component we determine the size of DISCONNECTED. Then our strong component algorithm gives us the size of SCC. We turn to our breadth-first search data. As noted, searching from a particular start node following a particular type of edges (in-edges or out-edges) would either terminate quickly, or grow the search to about 100M nodes. We say that a node explodes if it falls into the latter group. Thus, if a node explodes following in-links, and also explodes following out-links, it must be a member of a strong component of size at least 100M+100M-186M=14M. Since the second largest strong component is of size 150K, we infer that SCC is the unique strong component that contains all nodes exploding following in- as well as out-links. In fact, this observation contains two corroborating pieces of evidence for the structure in the figure above: first, it turns out that the fraction of our randomly chosen BFS start nodes that explode under in- and out-links is the same as the fraction of nodes in the SCC as returned by our SCC algorithm. Second, every BFS start node in the SCC reaches exactly the same number of nodes under in-link expansion -- this number is 99,807,161. Likewise, under out-link expansion every node of SCC reaches exactly 99,630,178 nodes.
Thus, we know that SCC + IN = 99,807,161, and similarly SCC + OUT = 99,630,178. Having already found the size of SCC, we can solve for IN and OUT. Finally, since we know the size of the giant weak component, we can subtract SCC, IN, and OUT to get TENDRILS. We now discuss each region in turn.
Similarly, we know that if we explore in-links from a node in OUT, or
out-links from a node in IN, we will encounter about 100M other nodes in
the BFS. Nonetheless, it is reasonable to ask: how many other
nodes
will we encounter? That is, starting from OUT (or IN), and following
in-links (or out-links), how many nodes of TENDRILS and OUT (or IN)
will we encounter? The results are shown below in the row labeled
"exploring inwards -- unexpected nodes". Note that the numbers in
the table represent averages over our sample nodes.
| Starting Point | OUT | IN |
| Exploring outwards -- all nodes | 3093 | 171 |
| Exploring inwards -- unexpected nodes | 3367 | 173 |
As the table shows, OUT tends to encounter larger neighborhoods. For example, the second largest strong component in the graph has size approximately 150K, and two nodes of OUT encounter neighborhoods a few nodes larger than this, suggesting that this component lies within OUT. In fact, considering that (for instance) almost every corporate website not appearing in SCC will appear in OUT, it is no surprise that the neighborhood sizes are larger.
| Measure | Minimum depth | Average depth | Maximum depth |
| In-links | 475 | 482 | 503 |
| Out-links | 430 | 434 | 444 |
As the table shows, from some nodes in the SCC it is possible to complete the search at distance 475, while from other nodes distance 503 is required. This allows us to conclude that the directed diameter of SCC is at least 28.
Likewise, for SCC the (min, average, max) depths for termination under out-links are (430, 434, 444). For OUT, the values are (430, 434, 444).
Now, consider the probability that an ordered pair (u,v) has a path from u to v. By noting that the average in-size of nodes in IN is very small (171) and likewise the average out-size of nodes in OUT is very small (3093), the pair has a path with non-negligible probability if and only if u is in SCC+IN, and v is in SCC+OUT. The probability of this event for node pairs drawn uniformly from our crawl is only 24%; for node pairs drawn from the weak component it is only 28%. This leads to the somewhat surprising conclusion that, given a random start and finish page on the web, one can get from the start page to the finish page by traversing links barely a quarter of the time.
The structure that is now unfolding tells us that it is relatively insensitive to the particular large crawl we use. For instance, if AltaVista's crawler fails to include some links whose inclusion would add one of the tendrils to the SCC, we know that the resulting change in the sizes of SCC and TENDRIL will be small (since any individual tendril is small). Likewise, our experiments in which we found that large components survived the deletion of nodes of large in-degree show that the connectivity of the web is resilient to the removal of significant portions.
We can estimate the average connected distance using our 570 BFS start
points, under both in-links and out-links. The values are shown below;
the column headed "Undirected" corresponds to the average undirected distance.
| Edge type | In-links (directed) | Out-links (directed) | Undirected |
| Average connected distance | 16.12 | 16.18 | 6.83 |
These results are in interesting contrast to those of [Albert, Jeong and Barabasi 99], who predict an average distance of 19 for the web, based on their crawl of the nd.edu site; their calculations are unclear on whether directed or undirected distances are considered. Our results on the other hand show that over 75% of time there is no directed path from a random start node to a random finish node; when there is a path, the figure is roughly 16. However, if links can be traversed in either direction, the distance between random pairs of nodes can be much smaller, around 7, on average.