Project: Valid dates
N pairs of brothers (a_1 b_1), (a_2 b_2), (a_3 b_3), ... , (a_N b_N) are to blind-date N pairs of sisters
(x_1 y_1), (x_2 y_2), (x_3 y_3), . . .,x_N y_N) such that any two brothers do not date two corresponding sisters. That is for example if (a_2,x_4) is a date then, b_2 cannot date y_4.
In how many ways can the dates be arranged?
Part A: Brute force
Describe (on paper) an algorithm that does all the valid pairings and counts them. Write the code accordingly to also print each valid date arrangement.
Part B: O(N) recurrent calculation
Say T(N) = the total number of valid dates for N brother-pairs ad N sister-pairs
Let R(N) is the number of valid dates for N pairs that form a cycle date-sibling-date-sibling etc. For example
N=2 a1-x1-y1-a2-b2-y2-x2-b1
N=3 a1-x1-y1-a2-b2-y3-x3-a3-b3-x2-y2-b1
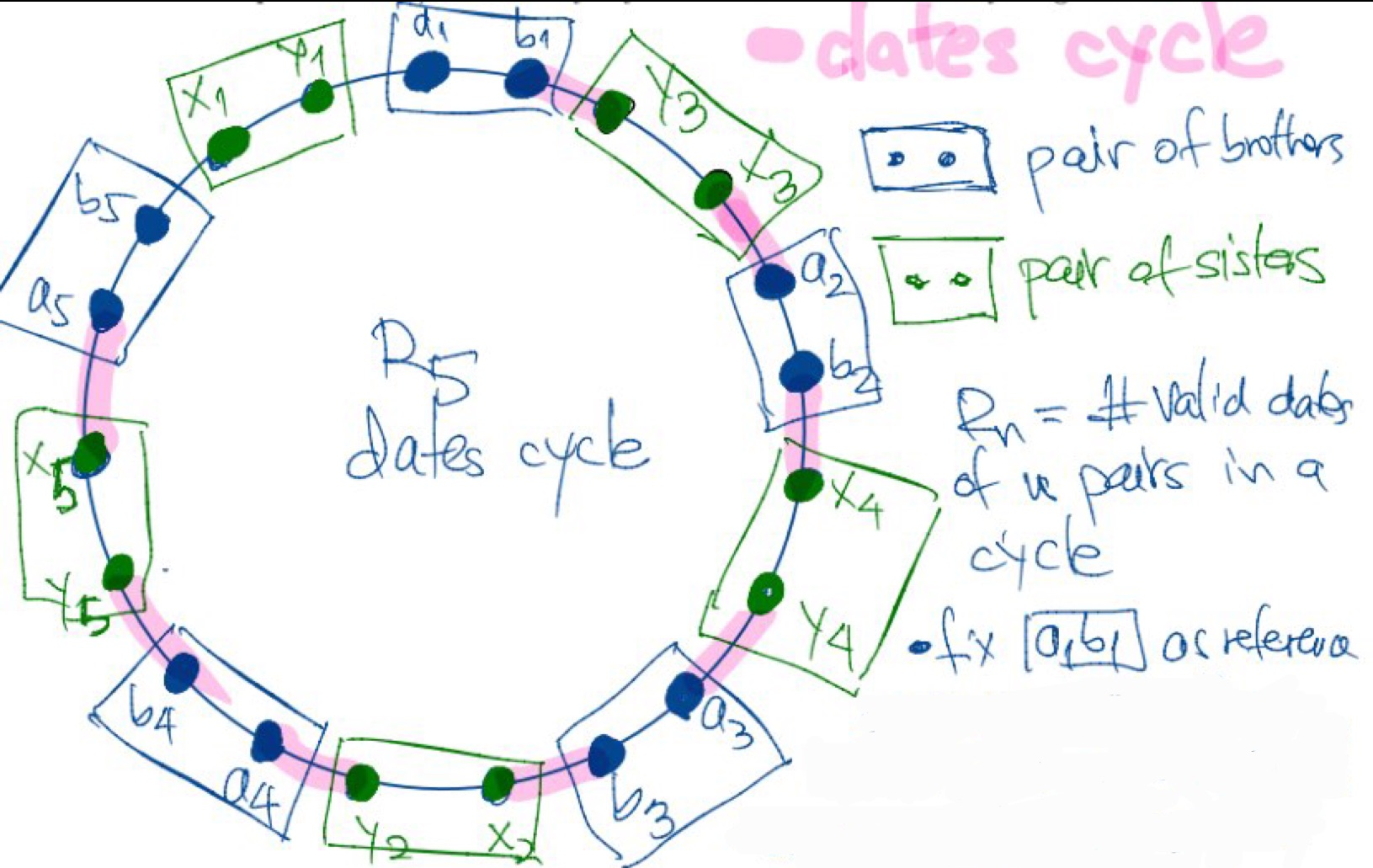
Compute R(N) in close form. There is also an easy recurrence R(N) = function (R(N-1))
Describe a combinatorial decomposition the count T(N) of valid-dates for N as a function of T(N-K) and R(K) for various possible K; these ways will have to be summed up, as they are disjoint cases. You will have to write this as a math proof.
Write bottom-up code to compute T(N) array from N=1:MAX using this recurrence. Due to the sum each T() computation will take O(N) steps; so O(N^2) total.
Part C : O(1) recurrent calculation
Describe a combinatorial decomposition of T(N) into a simple calculation based on T(N-1) and T(N-2) (math proof). Write code to compute T(N) as an array with this O(1) calculation per N, thus O(N) total
Results
| N | R(N) | T(N) |
| 1 | 0 | 0 |
| 2 | 16 | 16 |
| 3 | 384 | 384 |
| 4 | 18432 | 23040 |
| 5 | 1474560 | 2088960 |
| 6 | 176947200 | 278323200 |
| 7 | 29727129600 | 50969640960 |
| 8 | 6658877030400 | 12290021130240 |
| 9 | 1.9177565847552e+15 | 3.7743941910528e+15 |
| 10 | 6.90392370511872e+17 | 1.43842124570296e+18 |
