2CNF-SAT
The 2SAT-CNF instance is a boolean CNF formula with 2 variables in each clause. There are n boolean variables x_1 , x_2 , ..., x_n )
and several clauses; every variable and its negation appears in at least one clause. Such formula is given as input in a file format where each clause is a line with two integers corresponding to indices of variables. Negations are represented with negative indices.
For example formula (x1 ∨ ¬x2 ) ∧ (x2 ∨ x3 ) ∧ (¬x1 ∨ x3 ) ∧ (¬x2 ∨ ¬x3 ) is given as a file with 4 lines:
1 -2
2 3
-1 3
-2 -3
example_file
Test cases:
test0
test1
test2
test3
test4
test5
test6
test7
test8
Part A
Write a procedure on paper that determines the boolean assignments
for the variables such that all clauses are satisfied, thus the formula is true (if more
such assignments are possible, you only need to output one). If no such assignment
is possible, output ”FALSE”.
As established in the HW, there are 2^n possible assignments for the variable set.
So if one were to build the truth table and ”brute force” search all rows/assignments
until one works, it would take exponential time — not good! Instead: do trial and
error, but in a smart way that only tries at most about (2*n) boolean assignments, in no more than (4* clauses) steps.
Your program can be pseudocode, or you can informally describe a procedure with
bullets and English statements. You can write in your procedure statements like
* x = x1
* foreach clause (x ∨ y) containing variable x {
- do something with y
}
* put y into a list or queue
* z = next element in the queue
* assign x=T (or False)
* C = list of clauses containing x
etc
Part B
Load the input file and transform the formula into a graph with 2*N nodes: one for each variable and one for its negation. The clauses are represented as edges, each clause makes 2 edges!
2CNF_SAT_GraphHint
Represent the graph with an adjacent matrix (or adj list). Translate your procedure-on-paper in part (A) to actual code in Python or Matlab. The main idea is trial-and-error: start with a variable assignment and then follow "Truth" to the graph until either it works or a contradiction occurs.
Part C (optional, no credit)
Can you modify your program to work on 3SAT-CNF formula, where each clause has exactly 3 variables? How many trial assignments of the variables your program has to make to determine the satisfiable assignment?
Example 3SAT formula (x1 ∨ ¬x2 ∨ x3 ) ∧ (x2 ∨ x3 ∨ x4 ) ∧ (¬x1 ∨ x3 ∨ ¬x4 ) ∧ (¬x2 ∨ ¬x3 ∨ ¬x1 ) would be given as
1 -2 3
2 3 4
-1 3 -4
-2 -3 -1
Answer: probably not. This is an open question, one of the famous "P vs NP question" that most scientists think its not solvable in polynomial time; in other words only some form of brute force (exponential) is guaranteed to work in all cases.
See P VS NP on wikipedia and 3CNF-SAT problem .
Part D
Is it possible during your graph traversal (for trial assignments) to run into the situation illustrated in the picture below? That is:
- run 1: you start with assignment x=TRUE then propagate Truth to the graph eventually to all reachable nodes, including z. It means that not_Z must be assigned FALSE. You dont find a contradiction therefore you make this a permanent assignment.
- run 2: since not all variables were assigned, you start again from y=TRUE. The traversal from y eventually reaches not_z ; this is a problem since not_z is already FALSE but you need now to make it TRUE
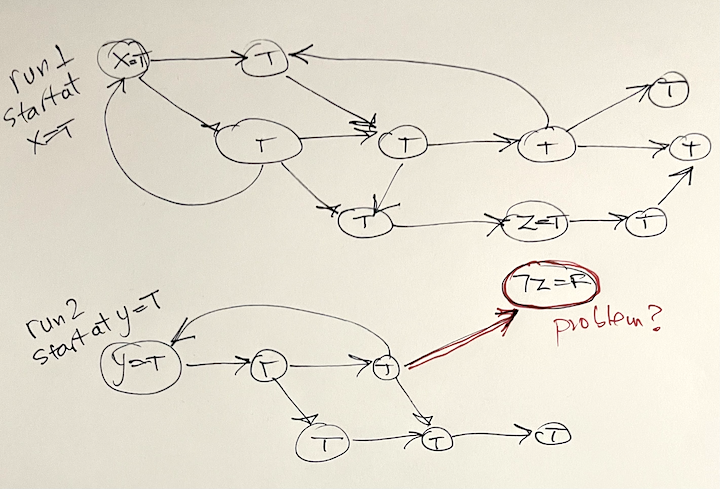
Is this a contradiction to declare "not possible"? or to try redoing the second run from not_y=TRUE? Or do you have to go back and redo the first run? Or simply this situation cannot happen foe 2CNF_SAT graphs?
If this can occur, explain how to deal with it. If not, proof (math) that its not possible.
