The lab is designed to provide extra questions for you to practise and as such you are not expected to finish the lab during our lab session. We recommend that you do eventually complete the lab on your own time.

1. Association List

We would like to design a program that implements an Association List [1] (AList). An AList contains pairs as elements. We will use {< >} to represent an empty AList and (k,v) to represent a pair.

  • The first element of the pair k is called a key.

  • the second element of the pair v is called a value.

So an AList holds key-value pairs. We would like to create an AList that has Point s as keys and Shape s as values. You can reuse your code for Point and Shape from previous Lectures/Labs/Assignments.

Here is a table of the operations along with their specifications and comments.

Operation Specification Comments

createEmpty() : AList

createEmpty() = {< >}

  • Creates an empty AList.

isEmpty: Boolean

 
{<>}.isEmpty()                    = true

{<(k,v), (k1,v1), ...>}.isEmpty() = false

  • returns true if the AList is empty

  • returns false if the AList is non-empty

size() : Integer

 
{<>}.size()                    = 0

{<(k,v), (k1,v1), ...>}.size() =
    1 + {<{k1,v1,...>}.size()

  • returns 0 if the AList is empty

  • returns the number of pairs in the AList

add(a,b): AList

 
{<>}.add(a,b)                    = {<(a,b)>}

{<(k,v), (k1,v1), ...>}.add(a,b) =
    {<(a,b), (k,v), (k1,v1),...>}

  • if the AList is empty returns a new AList with one pair (a,b)

  • if the AList is non-empty returns a new AList that has the same pairs in the same order as the original non-empty AList but with the pair (a,b) prepended

replace(a,b) : AList

 
{<>}.replace(a,b)                    = {<>}

{<(a,c), (k1,v1), ...>}.replace(a,b) =
    {<(a,b),(k1,v1),...>}

{<(x,c), (k1,v1), ...>}.replace(a,b) =
    {(k1,v1),...>}.replace(a,b).add(x,c)

  • if the AList is empty replace returns the empty AList

  • if the first pair of the AList has the same key as the key provided as argument, a then replace the value of the pair in the AList with the second argument b

delete(x) : AList

 
{<>}.delete(x)                    = {<>}

{<(x,v), (k1,v1), ...>}.delete(x) =
    {<(k1,v1), ...>}

{<(y,v), (k1,v1), ...>}.delete(x) =
    {<(k1,v1), ...>}.delete(x).add(y,v)

  • if the AList is empty delete returns the empty AList

  • if the first pair of the AList has the same key as the key provided as argument, a then remove the first pair and return the remaining AList unaffected.

  • if the first pair of the AList is not the same key as the key provided as argument, a then proceed to the rest of the pairs and keep the first pair as the first pair.

has(x): Boolean

 
{<>}.has(x)                    = false

{<(x,v), (k1,v1), ...>}.has(x) = true

{<(y,v), (k1,v1), ...>}.has(x) =
    {<(k1,v1), ...>}.has(x)

  • if the AList is empty return false

  • return true only if you find a pair in the AList that has the same key value as the argument x

get(x) : Shape

 
{<>}.get(x)                    = ERROR

{<(x,v), (k1,v1), ...>}.get(x) = v

{<(y,v), (k1,v1), ...>}.get(x) =
    {<(k1,v1), ...>}.get(x)

  • if the AList is empty then throw an error

  • else keep looking at each pair in the AList, the first pair whose key is the same as the argument x return the value from that pair
Practise Exercises

  • 1) Design a Java program that implements the AList ADT.

  • 2) A new client would like to alter some of the behaviour of AList. They would like you to provide an alternative implementation that when

    1. Calling replace on an empty AList should throw an error.

    2. Calling delete on an emptyu AList should throw an error.

      Implement this new implementation of AList. Can we provide your new implementation to AList to our original clients without breaking our original clients, or requiring them to alter their code? Explain your answer

2. Binary Trees

An Integer BinaryTree (IBT) comprises of a leaf or a node. Both a leaf and a node contain an integer value. A node however also contains two sub trees called the left and the right subtree.

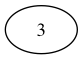
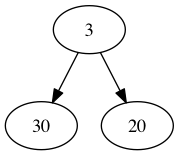
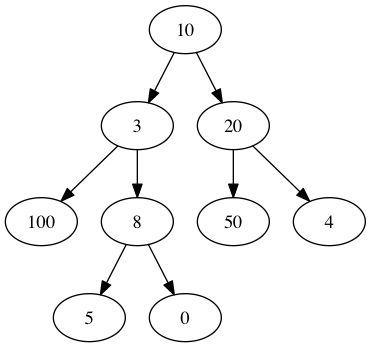
Here are some examples of IBTs

Table 1. Examples of IBTs.
Ex1 Ex2 Ex3
treeexamples
node1
node2
Practise Exercises

  • 3) Design a Java class hierarchy that captures IBTs.

  • 4) Create examples of IBTs.

  • 5) Design the following operations on an IBT.

    1. Design an operation size that returns the total number of nodes and leafs in the IBT.

    2. Design an operation sum that returns the sum of all integers found inside nodes and leafs of the tree.

    3. Design an operation multiply that returns the product of all integers found inside nodes and leags of the tree.

    4. Design an operation contains that takes as input an integer element and returns true if element is found as a value inside a node or a leaf of the IBT and false is element is not found as a value inside a node or leaf of the IBT.

    5. Design an operation add that takes as input three integers existingLeaf, newLeftLeaf and newRightLeaf. The operation locates the leaf in the IBT that contains the same integer value as existingLeaf and turns it into a node that contains existingLeaf as its value and a new leaf that contains newLeftLeaf as its left sub-tree and a new leaf that contains newRightLeaf as its right sub-tree.

      For example calling add(3, 30, 20) on Ex1 in Table 1, should return the tree in Ex2 found in Table 1.

      If the first argument to add is an integer that is not in the tree or it is a node and not a leaf, your implementation should signal an error.

We would like to create a string representation of our our IBTs using the following rules

  1. For a leaf create a string with

    1. the integer value inside the leaf

  2. For a node create a string with

    1. a left parenthesis first.

    2. the integer value stored at this node.

    3. a space.

    4. its left-subtree.

    5. a space

    6. the right subtree.

    7. a right parenthesis.

The table below shows how the IBTs from above get printed out

Pretty print Leaf example

Pretty print Node example

Pretty print Node example

3

(3 30 20)

(10 (3 100 (8 5 0)) (20 50 4))
Practise Exercises

  • 6) Design the operation asString for IBTs that when called on an IBT returns a String formatted based on the preceding requirements.

  • 7) Design a new tree called STree, where the leafs contain an integer value but the nodes contain a String value and a left and a right STree. Implement asString using the same formatting rules as above. Does the return value of asString on STree look familiar?

1. Association lists are one implementation for a key-value data structure. In other languages these are called dictionaries or maps.