Relevant Reading Material
Code Style
We will follow the Google Style Guide. The lab will have a section on how to configure your IDE.
Recursive Data
Recall Racket Lists
Using an itemization, structs and a self reference.
+-------------+
\/ |
;; A List of Number (LoN) is one of |
;; - empty |
;; - (cons Number LoN) --------------+
;;lon-size: LoN -> Number
+---------------+
\/ |
(define (lon-size alon) |
(cond |
[(empty? alon) 0] |
[(cons? alon) (+ 1 (lon-size (rest alon)))]))Now in Java
Same idea, itemization, classes and a self reference
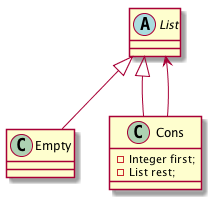
Adding a size() operation will require the following modifications
-
Add
abstractmethodInteger size()onList -
Implement
size()in each of the subclassesEmptyandCons
Here is the updated uml diagram
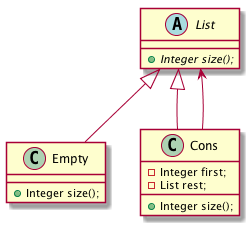
Lets also add the following methods
-
a method called
List add(Integer num)that addsnumto the beginning of the list. -
a method called
Integer last()that returns the last element of the list -
a method called
List addToEnd(Integer element)that adds the given element to the end of the list -
a method called
Integer elementAt(Integer index)that returns the element at indexindex
Exceptions
An exception is an event that occurs during execution of a program and disrupts the normal flow of execution.
| Diagram of call stack and what exceptions do. |
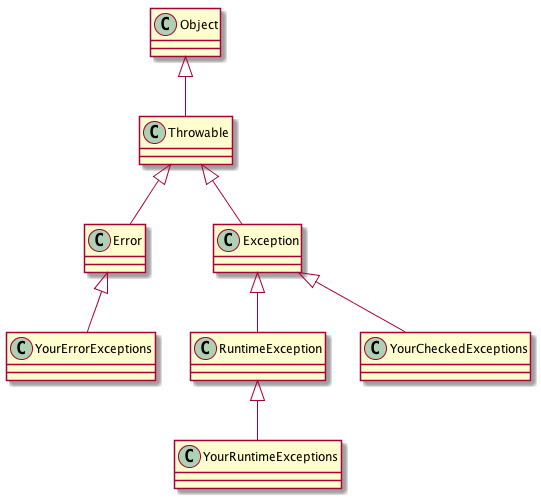
Three kinds of exceptions
-
Checked Exceptions capture events that a well-written application must anticipate and recover from.
-
opening a file using the file name provided by the user and cannot find that file
-
opening a connection to a server whose address was provided to the program by an external entity
-
-
Errors capture exceptional conditions external to the application that the application cannot anticipate or recover from.
-
error reading from the disk
-
error reading from the connection to the database
-
-
Runtime Exception captures events that are exceptional and internal to the application. The application typically cannot anticipate them or recover from
-
passing in the incorrect values for the arguments to a function
-
logical errors; going over the length of a list
-
Java provides special syntax to mark code that could throw an exception as well as catching an exception.
try {
// try to run these expressions/statements that may throw an exception
} catch (ExceptionType ext) {
// catch an exception of type ExceptionType, bind it to the variable ext
// perform actions to recover
} catch (ExceptionType2 ext2) {
// catch an exception of type ExceptionType2, bind it to the variable ext2
// perform actions to recover
} catch (IOException | SQLException ex) {
// catching multiple exceptions for which we deal with in the same
// way
}Syntax to declare that a method can throw an exception (of any kind)
public Integer method() throws RuntimeException, ArgumentException {
}Java’s exception hierarchy
Lets create an exception and add it to the method Integer elementAt(Integer index).
Testing methods that throw exceptions in JUnit
JUnit can be used to check your methods even under conditions that throw exceptions.
To tell JUnit that you expect an exception to the thrown we add to the @Test annotation
the expected exception
@Test(expected=MyException.class)
public void testElementAt() {
//call the method in a way that causes an the expected exception to be thrown
}Abstract Data Types (ADT)s
After adding all these methods we should obtain a class diagram that looks like

There is a pattern here!
-
An Abstract Data Type (ADT) refers to a model that describes data by specifying the operations that we can perform on them.
-
A Data Structure refers to the concrete implementation (the details).
-
Users care about the ADT.
-
Developers care about the data structure (it’s memory consumption, speed, correctness) and how the inner workings of the data structure satisfy the ADT.
This is why you will often here about the public interface and the private interface of a data.
The List ADT
We are going to use (()) to denote an empty list. To show a non-empty
list we will place the elements of the list inside the parenthesis
separated by commas.
| Operation | Specification | Comments |
|---|---|---|
|
|
Creates an empty list |
|
(()).isEmpty() = true ((1,2,...)).isEmpty() = false |
|
|
(()).add(1) = ((1)) ((1,2,...)).add(0) = ((0,1,2,...)) |
|
|
(()).contains(1) = false ((1,2,...)).contains(1) = true ((1,2,...)).contains(x) = ((2,...)).contains(x) |
|
|
(()).size() = 0 ((1,2,...)).size() = 1 + ((2,...)).size() |
|
|
(()).elementAt(n) = ERROR ((1,2,...)).elementAt(0) = 1 ((1,2,...)).elementAt(n) = ((2,...)).elementAt(n - 1) |
|
|
(()).tail() = ERROR ((1,2,...)).tail() = ((2,...)) |
|
The specification is a logical/mathematical description of what the operation does not how to do it.
-
The clients only cares about what each operation does.
-
The developer needs to
-
understand what each operation should do
-
design a program that implements the specification
-
Liskov substitutability principle
In our designs we have used the property that a subclass can be used in the place of the super class.
With ADTs we also need to ensure that the behaviour of our subclasses is compatible with the behaviour of our superclass.
Types as Sets
A Java class defines two aspects of a type
-
data
-
behaviour
With ADTs we are interested in behaviour. Informally, and for the purpose of this discussion, we will map Java Classes to a set of values. A value is in the set of a type iff the value is create using the class' constructor or a subclass' constructor.
We can use logical formulae to
-
describe the conditions that we expect to hold true before calling a method. Conditions can refer
-
the state of our object
-
impose restrictions to the values passed as arguments
-
-
describe the conditions that we expect to hold true as soon as the method returns. Conditions can refer
-
to the return value
-
the relations of the return value and the original values passed as argument and/or the state of the object when the method was called
-
These conditions are called contracts. . The formulae that describes the conditions we expect to hold true before calling a method is called a pre-condition. . The formulae that describes the conditions we expect to hold true immediately after the method returns is called a post-condition.
| Operation | Specification | Contracts |
|---|---|---|
|
|
|
|
(()).isEmpty() = true ((1,2,...)).isEmpty() = false |
result -> this == (()) OR !result -> this != (()) |
|
(()).add(1) = ((1)) ((1,2,...)).add(0) = ((0,1,2,...)) |
result.size() == old.size() + 1 AND result.contains(ele) AND forall x( old.contains(x) && result.contains(x) ) |
|
(()).contains(1) = false ((1,2,...)).contains(1) = true ((1,2,...)).contains(x) = ((2,...)).contains(x) |
result -> (this.size() > 0 && exists x ( 0 <= x <= this.size() && this.elementAt(x).equals(ele))) |
|
(()).size() = 0 ((1,2,...)).size() = 1 + ((2,...)).size() |
result == |this|---- |
|
(()).elementAt(n) = ERROR ((1,2,...)).elementAt(0) = 1 ((1,2,...)).elementAt(n) = ((2,...)).elementAt(n - 1) |
|
|
(()).tail() = ERROR ((1,2,...)).tail() = ((2,...)) |
result.size() + 1 == this.size() AND result.add(this.elementAt(0)).equals(this) |
Liskov’s substitution principle states that for two types T and S such that S is a subtype of T, we should
be able to take existing client code that used T, and replacement with objects of type S without altering
breaking the clients contracts (pre- and post-conditions).
So if we have
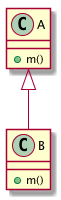
The logical implications that we need to ensure hold true are
-
A.mpre ⇒B.mpre and -
B.mpost ⇒A.mpost