List abbreviations
Our BSL provides us with an abbreviation (shorthand) to create lists. The abbreviation is a function called list and
we can use it to create non-empty lists. You should still use empty for the empty list.
> (list 1 2)
(cons 1 (cons 2 '()))More recursive data definitions; Trees
Lists are one of many data definitions that are recursive. Another popular data definition that uses recursion is a Binary Tree.
A binary tree is either an empty node that we call a leaf or a node (or non-leaf) that contains
-
a value; we will use
Numberfor our example -
a left child or left sub-tree
-
a right chilkd or right sub-tree
Here are some examples.

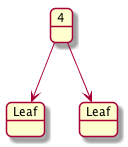
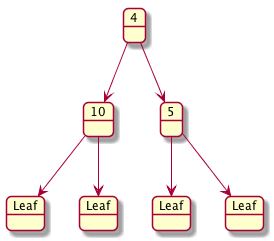
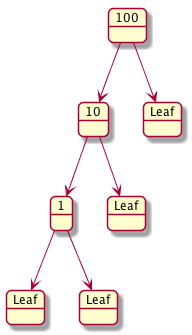
Here is a data definition for a BT
;;;; Data Definition:
(define-struct leaf ()) (1)
(define-struct node (value left right))
;; A BinaryTree (BT) is one of
;; - (make-leaf)
;; INTERP: represents an empty leaf node
;; - (make-node Number BT BT) (2)
;; INTERP: represents a node with a value and 2 children
;;
;;INTERP: represents a binary tree| 1 | A leaf is a struct that contains no slots |
| 2 | A node is a struct that contains the value and two slots that both have a BT. |
Let’s write down our deconstructor template
;; Deconstructor Template:
;; bt-fn: BT -> ???
#; (define (bt-fn bt)
(cond
[(leaf? bt) ...] (1)
[(node? bt) ... (node-val bt) ... (2)
... (bt-fn (node-left bt)) ... (3)
... (bt-fn (node-right bt)) ...])) (4)| 1 | when we are given a leaf, eventhough it is a structure, the structure has not slots and thus nothing more to deconstruct here |
| 2 | when we are given a node however we have the node’s value which is a scalar |
| 3 | the node’s left sub-tree which is a BT again. So we have to keep deconstructing this BT. We have a deconstructor for BT it’s the one we are currently
in the process of writing, so add a call back to bt-fn |
| 4 | the node’s right sub-tree which is a BT again. So we have to keep deconstructing this BT. We have a deconstructor for BT it’s the one we are currently
in the process of writing, so add a call back to bt-fn |
Observer how there are two recursive calls just like there are two recursive definitions in our BT data definition
Now that we have a data definition for BT let’s try and design a program that will take in a BT and return the sum of all the values in the BT
;;;; Signature:
;; bt-sum: BT -> Number
;;;; Purpose:
;; GIVEN: a binary tree
;; RETURNS: the sum of the binary trees values
(define LEAF (make-leaf))
;;;; Examples:
;; (bt-sum LEAF) => 0
;; (bt-sum (make-node 1 LEAF LEAF)) => 1
;; (bt-sum (make-node 2 (make-node 1 LEAF LEAF)
;; (make-node 3 LEAF LEAF)))
;; => 6
;;;; Function Definition:
(define (bt-sum bt)
(cond
[(leaf? bt) 0] (1)
[(node? bt) (+ (node-value bt) (2)
(bt-sum (node-left bt)) (3)
(bt-sum (node-right bt)))])) (4)
;;;; Tests:
(check-expect (bt-sum LEAF) 0)
(check-expect (bt-sum (make-node 1 LEAF LEAF)) 1)
(check-expect (bt-sum (make-node 2 (make-node 1 LEAF LEAF)
(make-node 3 LEAF LEAF)))
6)| 1 | when we are given a leaf then the sum is 0 |
| 2 | when we are given a node we would like to extract the number stored in the slot value and add it to |
| 3 | the sum of our left sub-tree and |
| 4 | the sum of our right sub-tree. |
Observe how there are two recursive calls just like there are two recursive calls in our deconstructor template
Let’s try another function. Let’s try to design a function that given a BT and a number will tell us if the number is already in the BT or not.
;;;; Data Definitions: none
;;;; Signature:
;; bt-contains?: BT Number -> Boolean
;;;; Purpose:
;; GIVEN: a binary tree and a number
;; RETURNS: true if the number is found within the binary tree
;; false otherwise
(define BT-LARGE (make-node 10
(make-node 7
(make-node 2 LEAF LEAF)
(make-node 100 LEAF (make-node 1 LEAF LEAF)))
(make-node 0
(make-node 20
(make-node 2 LEAF LEAF)
(make-node 30 LEAF LEAF))
LEAF)))
;;;; Examples
;; (bt-contains? (make-leaf) 3) => #false
;; (bt-contains? (make-node 1 LEAF LEAF) 1) => #true
;; (bt-contains? BT-LARGE 30) => #true
;; (bt-contains? BT-LARGE 888) => #false
;; (bt-contains? BT-LARGE 2) => #true
;;;; Function Definition
(define (bt-contains? bt element)
(cond
[(leaf? bt) #false]
[(node? bt) (or (= element (node-value bt))
(bt-contains? (node-left bt) element)
(bt-contains? (node-right bt) element))]))
;;;; Tests
(check-expect (bt-contains? (make-leaf) 3)
#false)
(check-expect (bt-contains? (make-node 1 LEAF LEAF) 1)
#true)
(check-expect (bt-contains? BT-LARGE 30)
#true)
(check-expect (bt-contains? BT-LARGE 888)
#false)
(check-expect (bt-contains? BT-LARGE 2)
#true)Binary Search Trees
Another popular variation of the Binary Tree is the Binary Search Tree (BST). A BST is similar to a BT but it also has to satisfy the following condition
For each node in the BST that is not a leaf node the value stored at the node \(v\) is
-
greater than all values found in the left sub_tree, and
-
less than all the values found in the right sub-tree.
We will later see BSTs that may contain something other than just integers, but, for now we will stick to integer BSTs.
Let’s draw some examples and detect if they are BSTs.

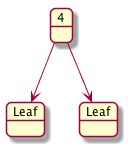
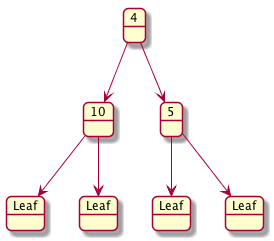
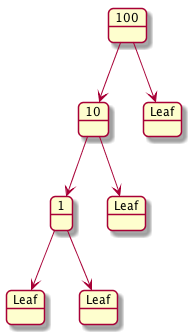
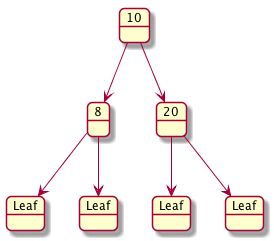
Let’s design a data definition for an Integer (IBST)
;;;; Data Definition:
(define-struct leaf ())
(define-struct node (value left right))
;; A IntegerBinarySearchTree (IBST) is one of
;; - (make-leaf)
;; INTERP: represents an empty leaf node
;;
;; - (make-node Integer IBST IBST)
;; WHERE: value is greater than all values in the left subtree and
;; value is less than all values in the right subtree
;; INTERP: represents a node with a value and 2 children
;;
;;INTERP: represents a binary search tree
;; Deconstructor Template:
;; bst-fn: BST -> ???
#; (define (bst-fn bst)
(cond
[(leaf? bst) ...]
[(node? bst) ... (node-val bst) ...
... (bst-fn (node-left bst)) ...
... (bst-fn (node-right bst)) ...]))The data definition for IBST is similar to BST but not exactly the
same. IBST 's data definition includes extra conditions, the exact
conditions that make a BT a BST.
So a BST is always a BT as well, but, a BT is not always a BST.
This property of the BST is very useful. For some operations over a BST we can be smarter on how we proceed down the left and/or right subtrees. For example, if we are trying to find a number in our BST we can take advantage of the fact that numbers to the left of a node are less than the number at the current node and numbers to the right of the node are greater than the number at the current node and save ourselves some work and time.
Animations and big-bang
See Slides pdf