Midterm Exam - CSU540 Computer Graphics - Spring 2005
Given on February 22nd 2005 -- Professor Futrelle
This is a closed book, closed notes exam.
Put your answers and all your calculations in your Blue Book.
No calculator is
needed or should be used.
In drawing diagrams including fractional values, a reasonable approximation suffices.
When you are asked to do a transformation step-by-step, write, draw and, comment
on the results of each step. For diagrams, label all axes, coordinates,
points, and vectors.
For convenience in writing out your answers, vectors can be
written in row format,
as [x,y] or [x,y,z], and for homogeneous coordinates too,
in contrast to the book's column format.
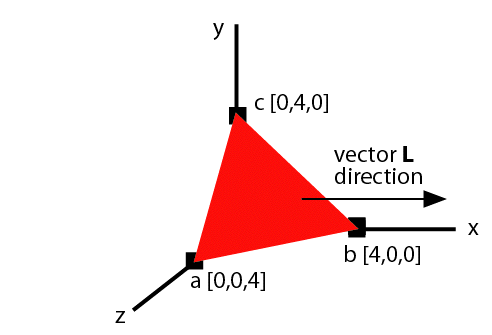
Question 1. Vector algebra. In the figure below,
the triangle a,b,c sits
symmetrically near the origin, with its outer surface directed
away from the origin, towards "you".
What you are to compute is the inner product
of the unit normal, N, to the triangle, with the vector
L = [1,0,0].
When you compute the unit normal, make sure that its magnitude and direction
make sense to you -- does your unit normal have the values it should, given
the figure?
This type of
computation is used in calculating the amount of illumination to a surface.
In such a case, the vector L would be a vector directed toward the
light source.
You should know that the normal is computed using the cross product of
edge vectors and you should know how to normalize a vector to create
one of unit length, then how to compute the inner product (by components).
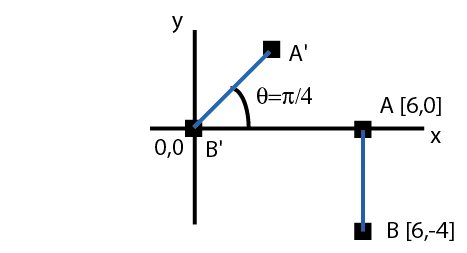
Question 2. Geometric transforms in two dimensions.
The figure below, shows a line A,B in its original position
and the line with corresponding points, A',B'
obtained by a pair of transforms, one a rotation
and the other a translation.
Your task it to create the translation and rotation matrices required,
T and R.
The transformations
can be designed to be applied in one order or designed with different values
to be applied in the other order, giving the same result.
(But you'll find that one order is simpler to design than the other.)
Do the following:
- Write out the your choice of T and R, indicating
why you chose the values you did as well as what order they must
be applied in.
- Apply the first matrix to be used to the two points
A,B and draw
the resulting diagram.
- Starting with that result, apply the second matrix and explain
why it results in the answer, A',B'.
- Multiply the two matrices together in the proper order
to produce a result M.
Apply M to the original points A,B and show
that it results in A',B'.
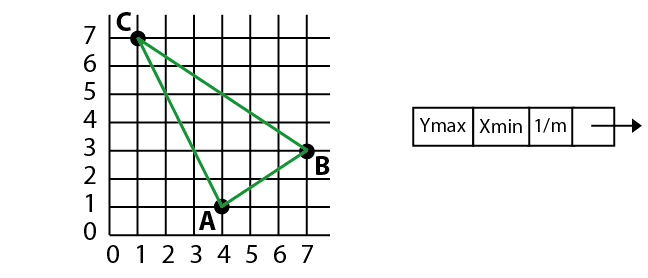
Question 3. Scan-fill of polygons.
The figure below, shows the triangle A,B,C.
To the right of it is the structure of one of the edge data elements.
Do the following two tasks:
- Build and draw the bucket-sorted edge table for the triangle,
starting with y=0.
- Show the active edge table (AET) for each of the
y values 1 through 7, seven drawings total.
In each AET update the Xmin value to the value at the
corresponding value of y.
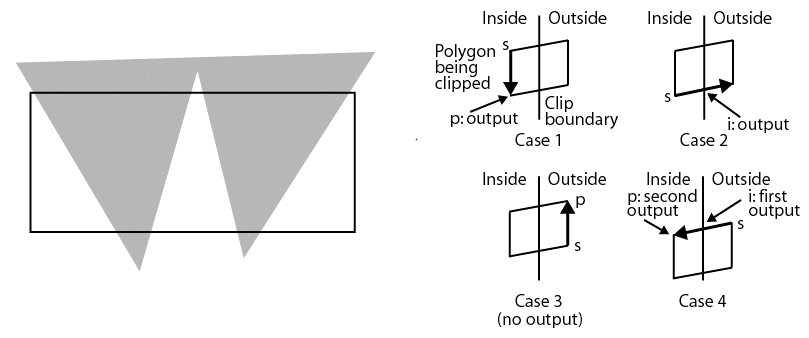
Question 4. Clipping polygons.
The figure below, shows a polygon that is to be clipped against
a rectangular window. The four cases are
illustrated to the right of the polygon figure.
Explain how each works.
Clip the polygon
in the order: bottom, top, right, and left for the window edges. Draw the
successive clipping steps as separate figures.
Question 5. Midpoint line algorithm for scan conversion.
The Java code below is an excerpt from a working version of the
Bresenham midpoint
algorithm for scan converting lines. You are to do the following:
-
- Write out the sequence of x,y pixel values that two calls
to the bres() method would draw. The first would be with
arguments 0,0,5,5 and the second call would be with
arguments 1,1,5,2. Include a comment or two,
in addition to just writing out the numbers.
- Compute the x,y points that would be generated for the two
lines by using the
standard formula y = mx + b and rounding the y values
you get for each x. Do not use a calculator, since all the values
will be simple fractions. Did your results agree with the values
from the Bresenham algorithm? (If there's an ambiguity
in rounding, go with the Bresenham value.)
The code (generated by the Code2HTML plugin in jEdit):
public void dobres(int x0, int y0, int x1, int y1){
int y = y0;
int d = 2*(y0 - y1)*(x0 + 1) + (x1 - x0)*(2*y0 + 1) +
2*x0*y1 - 2*x1*y0;
for (int x = x0; x <= x1; x++) {
draw(x,y);
if (d < 0)
{ y++;
d += 2*(x1 - x0) + 2*(y0 - y1);}
else
d += 2*(y0 - y1);
}
} // dobres()



