Below are the topics from the course schedule that are relevant to the Midterm Exam.
The exam questions will be similar the ones below.
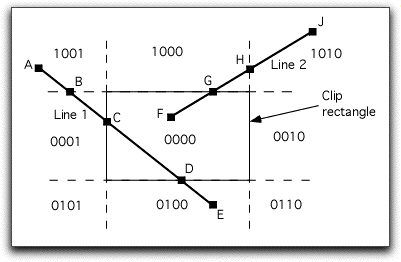
Question 1: The figure below shows two lines that need to be clipped to the rectangular window shown, using the Cohen-Sutherland algorithm. The outcodes are shown also, in the order TBRL. Describe each step in the process of clipping line AE. Then do the same for line FJ. (Pay attention to the TBRL order in these steps.)

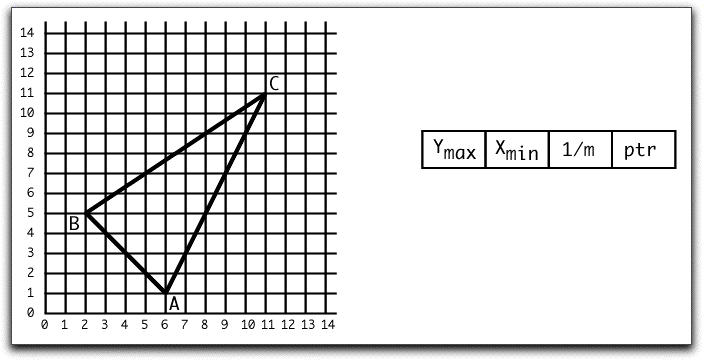
Question 2: The figure below shows a triangle that is to be filled using the scan line algorithm. The edge table element structure is shown to the right. You are to describe the two edge table elements that exist at run time when the filling has reached the line y = 7, where BC has the x value 5 and AC has the x value 9. Give the values of the four fields in each of the elements at this point. In addition explain briefly how you arrived at the values.
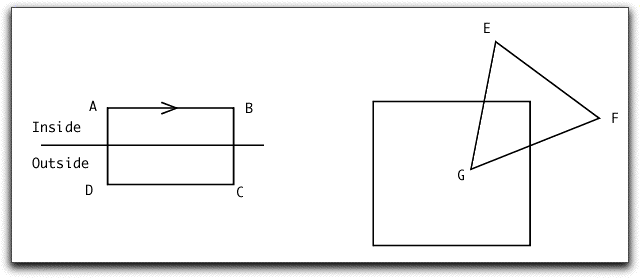
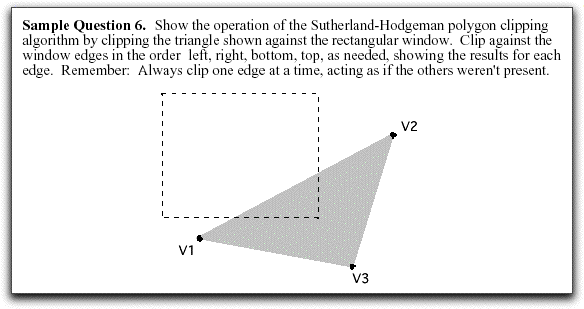
Question 3: On the left of the figure below is an example to illustrate the four cases encountered in clipping a region to one edge of a window using the Sutherland-Hodgman algorithm. As each of the edges are traversed, starting at A, tell what points are output to form the resulting clipped region. Next, use these rules to clip the triangle shown to its rectangular window, first clipping against the right rectangle boundary and then against the top boundary.
Question 4: This problem requires that you go through the steps of the stack-based fill algorithm. Starting at the gray double circle, fill the region. Use the same sequence as the book, looking above and to the right first, then left then down, etc. Do not redraw the entire figure for each scan line done. Just put a number at each pixel location where a point is stacked. Number every special point (stack entry) with a distinct number and show the stack at each stage (draw repeated views of the stack).

Midpoint line scan-conversion: You would be given the algorithm of Fig. 3.8 in the book. Be able to iterate it to produce filled pixel locations such as the ones in Fig. 3.9.
Cohen-Sutherland line clipping: Be able to apply the Cohen-Sutherland line clipping algorithm, Sec. 3.12.3. You would be given the region outcodes of Fig. 3.39. The important idea is that the clipping of a line is done by testing the outcodes, creating new endpoints as needed and continuing until nothing more needs to be done.
Sutherland-Hodgman polygon clipping: Be able to apply the Sutherland-Hodgman polygon clipping algorithm for polygons that may require clipping against more than one boundary, Sec. 3.14.1.This former question focused on clipping the five-sided polygon shown below against the upper edge of a rectangular window. The Sutherland-Hodgman polygon clipping algorithm creates a single polygon and in this case will produce a spurious line along part of the upper boundary. Only consider clipping against the upper window edge in this question.
Below is another earlier sample question on span-based filling (it is an image clipped from a PDF I had prepared):

Below is another image of an earlier sample question, this one on polygon clipping:
Q3. In the diagram below, a Bézier curve is to be drawn from P1 to P4 using control points P2 and P3 which are both located at 0,8.
Use the cubic Bézier formula for the curve:
Q(t) = (1 - t)3 P1 + 3t(1 - t)2 P2 + 3t2(1 - t) P3 + t3 P4
and apply it to the following figure. In particular, compute the x,y coordinates of the point on the curve at t = 1/2. By symmetry, this point should lie along the line from 0,8 to 8,0. Does it? Describe the convex hull of the four control points. Is the point you computed within this hull?
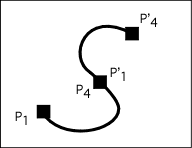
Q4. For the curve below, made up of two cubic Bézier curves, draw the control points P2, P3, P'2 and P'3, arranged in such a way that the curve directions at P1 and P'4 are correct and their is no discontinuity in the curve slopes at the meeting point P4, P'1.