Ray-Tracing Formulas

Ray - Sphere Intersection

A sphere is given by its center (cx, cy, cz) and its radius, R.

A line segment (ray) is given by its endpoints: P0 = (x0, y0, z0) and P1 = (x1, y1, z1).

To find visible spheres, set P0 = viewer coordinates = (Vx, Vy, Vz) and let P1 run through all the points (x1, y1, 0) where (x1, y1) is in the display area.

Set dx = x1 - x0

dy = y1 - y0

dz = z1 - z0

a = dx*dx + dy*dy + dz*dz;

b = 2*dx*(x0-cx) + 2*dy*(y0-cy) + 2*dz*(z0-cz);

c = cx*cx + cy*cy + cz*cz + x0*x0 + y0*y0 + z0*z0 +

-2*(cx*x0 + cy*y0 + cz*z0) - R*R;

discriminant(a, b, c) = b^2 - 4ac

if discriminant (a, b, c) < 0 no intersection

= 0 ray is tangent to sphere

> 0 ray intersects sphere in two points

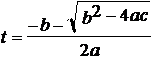
The intersection nearest P0 is given by:

To find the coordinates of the intersection point:

x = x0 + tdx y = y0 + tdy z = z0 + tdz

Ray-Tracing Steps

For each pixel in your image

1. Find the visible surface

Use the Ray-Sphere Intersection formulas with

P0 = Viewer = (Vx, Vy, Vz)

P1 = pixel = (x1, y1, 0)

Intersect this ray with each sphere in your scene

If no sphere intersects set the pixel to the background color.

Otherwise set the pixel to the color of the sphere that gave the intersection with the smallest t.

If you do only this, your picture should look like a number of overlapping disks on the plane.

2. Add Diffuse Shading

Do step 1 but replace the "Otherwise" with this:

Otherwise

Find the coordinates of the point (x, y, z) on the sphere.

x = x0 + tdx y = y0 + tdy z = z0 + tdz

Find the unit normal vector to the sphere at (x, y, z)

N = ((x - cx)/R, (y - cy)/R, (z - cz)/R)

Find a unit vector from (x, y, z) to the light (Lx, Ly, Lz).

where L' = (Lx - x, Ly - y, Lz - z).

Compute factor = N·L = cos of the angle between N and L.

Set the pixel to (kd*factor*R, kd*factor*G, kd*factor*B).+ (ka*R, ka*G, Ka*B).

where kd is the diffuse-coefficient and ka is the ambient-coefficient. (Try kd = .9 and ka = .1)

3. Find the Shadows

If the pixel is background color, use the Ray-Sphere Intersection formulas with

P0 = pixel = (x0, y0, 0)

P1 = Light = (Lx, Ly, Lz)

Intersect this ray with each sphere in your scene.

If there is any intersection, the pixel is in shadow.

Use half (or less) the R, G, B of your background color.

If there is no intersection, use the full R, G, B of the background color.

If the pixel is about to be colored to show a sphere, use the Ray-Sphere Intersection formulas with

P0 = Point on sphere = (x, y, z)

P1 = Light = (Lx, Ly, Lz)

Intersect this ray with every other sphere in your scene.

If there is any intersection, the point is in shadow. Use just the ambient color of the visible sphere.*

(ka*R, ka*G, Ka*B).

If there is no intersection, use the color computed in part 2.

(kd*factor*R, kd*factor*G, kd*factor*B).+ (ka*R, ka*G, Ka*B).

*Though it is not as physically correct, I sometime use

(.5*kd*factor*R, .5*kd*factor*G, .5*kd*factor*B).+ (ka*R, ka*G, Ka*B)

for points on the spheres that are in shadow. The makes the sphere look more rounded.